Задачи на оптимальный выбор – часть экономических задач, требующая хороших знаний о функциях и их свойствах. Чаще всего при решении таких задач требуется найти наибольшее или наименьшее значение составленной функции. Для этого можно использовать производную функции, а можно некоторые дополнительные знания: вспомогательные неравенства (неравенство о средних, неравенство об обратных величинах и д.р.), известные точки минимума и максимума функции и пр.

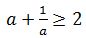
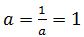
В разборе следующей задачи мы обошлись без производных, используя для нахождения наименьшего значения функции классическое неравенство:  при положительных значениях а, равенство возможно только при   .

Задача: Алек­сей вышел из дома на про­гул­ку со ско­ро­стью v км/ч. После того, как он про­шел 6 км, из дома сле­дом за ним вы­бе­жа­ла со­ба­ка Жучка, ско­рость ко­то­рой была на 9 км/ч боль­ше ско­ро­сти Алек­сея. Когда Жучка до­гна­ла хо­зя­и­на, они по­вер­ну­ли назад и вме­сте воз­вра­ти­лись домой со ско­ро­стью 4 км/ч. Най­ди­те зна­че­ние v, при ко­то­ром время про­гул­ки Алек­сея ока­жет­ся наи­мень­шим. Сколь­ко при этом со­ста­вит время его про­гул­ки?