Конспект занятия "Задача 15 (С 3). Показательные и логарифмические неравенства."
Показательные неравенства
Показательным называют неравенство, содержащее переменную в показателе степени некоторого положительного числа.
Теорема: Сравнение 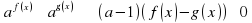 , где знак
, где знак  заменяет один из знаков
заменяет один из знаков 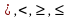 .
.
Методы решения произвольных показательных неравенств .
А. Метод уравнивания оснований.
1. Решите неравенство: 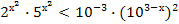 .
.
В. Метод решения, основанный на разложении на множители.
2. Решите неравенство: х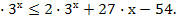
3. Решите неравенство: 3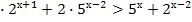 .
.
С. Метод введения вспомогательной переменной.
С помощью подстановки 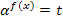 , где t
, где t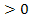 , неравенство приводится либо к квадратному неравенству относительно переменной t, либо к какому-нибудь другому неравенству относительно переменной t, решается относительно t , а затем ищется значение переменной х.
, неравенство приводится либо к квадратному неравенству относительно переменной t, либо к какому-нибудь другому неравенству относительно переменной t, решается относительно t , а затем ищется значение переменной х.
4. Решите неравенство: 4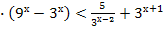 .
.
D. Неравенства, левая часть которых имеет вид А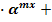 B
B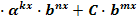 ,
,
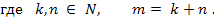
Неравенства такого типа решаются с помощью деления обеих частей на
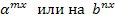 .
.
5. Решите неравенство: 3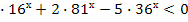 .
.
Е. Графический способ решения.
При решении неравенств графическим способом необходимо рассмотреть две функции, построить их графики в одной системе координат и выяснить при каких значениях аргумента значения одной функции больше (меньше) значений другой функции. Найденные значения аргумента и есть решения неравенства.
6. Решите неравенство: 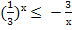 .
.
Задачи для самостоятельного решения.
Решите неравенство: 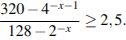
Решите неравенство: 
Решите неравенство: 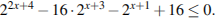
Решите неравенство 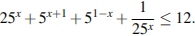
Решите неравенство
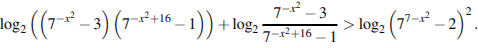
Решите неравенство: 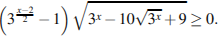
Решите неравенство: 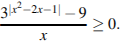
Решите неравенство: 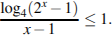
Решите неравенство: 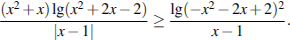
Решите неравенство 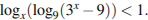
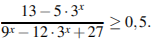
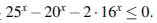
![]()


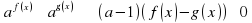 , где знак
, где знак  заменяет один из знаков
заменяет один из знаков 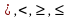 .
.