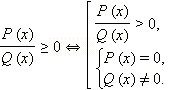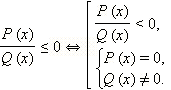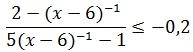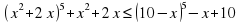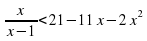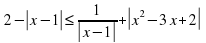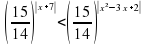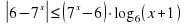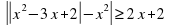Конспект занятия "Задача 15 (С3). Рациональные неравенства. Методы решения уравнений и неравенств с модулем."
Решенте рациональных неравенств
Рассмотрим стандартный приём решения рациональных неравенств, основанный на сведении данного неравенства к неравенству для многочлена, метод решения которого (метод интервалов) нам уже известен. Итак, рассмотрим рациональное неравенство
где f (x) и g (x) − рациональные функции, то есть функции, представимые в виде отношения многочленов. Перенося обе части рационального неравенства в левую часть, представим её в виде отношения двух многочленов: 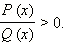 (Такой вид неравенства называется стандартным.)
(Такой вид неравенства называется стандартным.)
Привести неравенство к стандартному виду 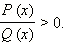
Разложить на множители многочлены P (x) и Q (x) (как мы знаем, для этого придётся решить уравнения P (x) = 0 и Q (x) = 0).
Нули числителя, не совпадающие с нулями знаменателя, отметить на числовой оси точками, а нули знаменателя − кружочками (эти точки, очевидно, не входят в ОДЗ рациональной функции и потому они как будто «выколоты» из числовой оси).
Подставить мысленно в неравенство очень большое число (большее самого большого из корней числителя и знаменателя) для того, чтобы определить, какой знак имеет рациональная функция на самом правом интервале. Провести кривую знаков, проходя через все точки, отмеченные на числовой прямой, меняя или не меняя знак в зависимости от суммарной степени двучлена, отвечающего данной точке.
Записать ответ, обращая особое внимание на граничные точки, часть из которых может быть «выколота».
Таким образом, для нестрогих рациональных неравенств имеем по определению
Решение неравенств, содержащих выражение под знаком модуль
Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Только, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.
Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки, границами этих промежутков являются нули подмодульных выражений, а затем неравенство решается на каждом из промежутков.
Этот метод работает всегда. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях ЕГЭ, где важен не только результат, но и то время, которое потрачено на его получение. Рассмотрим методы, не связанные с поиском нулей функций, стоящих под знаком модуля.
Решение неравенств с модулем:
1) |x+a|≤b⇔−(b+a)≤x≤b−a, где a0,b0a0,b0
2) |x+a|≥b⇔x≤−(a+b) или x≥−(a−b), где a0,b0a0,b0
3) x2≤a2⇔|x|≤a, a0 ⇔ −a≤x≤a
4) x2≥a2⇔|x|≥a,a0⇔x≤−a или x≥a .
5) |f(x)|⇔f2(x)2⇔(f(x)−k)⋅(f(x)+k)⇔f2(x)⇔(f(x)−k)⋅(f(x)+k)
6) Неравенства вида |f1(x)|+|f2(x)|≤|f3(x)| содержащие алгебраическую сумму двух и более модулей, решают методом промежутков:
разобьем числовую ось точками, в которых обращаются в нуль выражения, стоящие под знаком модуля.
выбирая на этих промежутках контрольные точки, проверяем, удовлетворяется ли на них заданное неравенство или нет.
ответом к задаче служит объединение промежутков, где выполняется данное неравенство.
Задачи к теме:
Решите неравенство 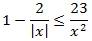
Решите неравенство 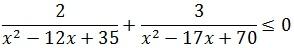
Решите неравенство 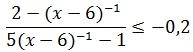
Решите неравенство 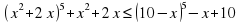
Решите неравенство 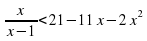
Решить неравенство: 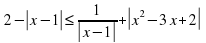
Решить неравенство: 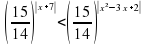
Решить неравенство: 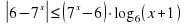
Решить неравенство: 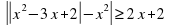
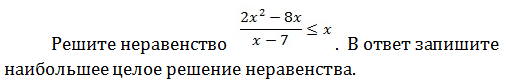




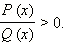 (Такой вид неравенства называется стандартным.)
(Такой вид неравенства называется стандартным.)