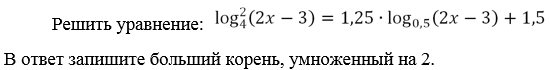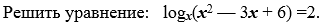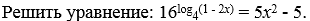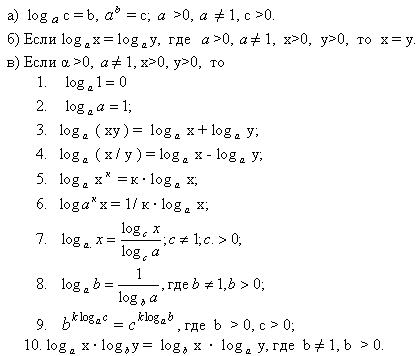Решение логарифмических уравнений.
Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма. При решении логарифмических уравнений часто используются теоретические сведения:
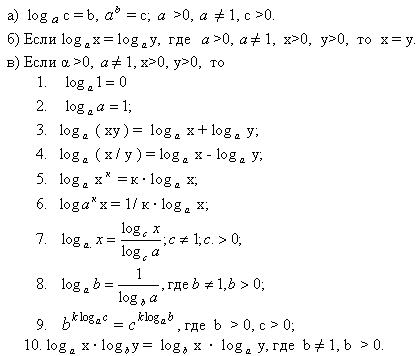
Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
Утверждение 1. Если a 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab.
Приведем основные свойства логарифма.
P1. Основное логарифмическое тождество:
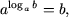
где a 0, a ≠ 1 и b 0.
P2. Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
loga N1·N2 = loga N1 + loga N2 (a 0, a ≠ 1, N1 0, N2 0).
Замечание. Если N1·N2 0, тогда свойство P2 примет вид
loga N1·N2 = loga |N1| + loga |N2| (a 0, a ≠ 1, N1·N2 0).
P3. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя
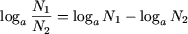 (a 0, a ≠ 1, N1 0, N2 0).
(a 0, a ≠ 1, N1 0, N2 0).
Замечание. Если 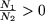 , (что равносильно N1N2 0) тогда свойство P3 примет вид
, (что равносильно N1N2 0) тогда свойство P3 примет вид
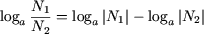 (a 0, a ≠ 1, N1N2 0).
(a 0, a ≠ 1, N1N2 0).
P4. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
loga N k = k loga N (a 0, a ≠ 1, N 0).
Замечание. Если k - четное число (k = 2s), то
loga N 2s = 2s loga |N| (a 0, a ≠ 1, N ≠ 0).
P5. Формула перехода к другому основанию:
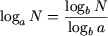 (a 0, a ≠ 1, b 0, b ≠ 1, N 0),
(a 0, a ≠ 1, b 0, b ≠ 1, N 0),
в частности, если N = b, получим
| 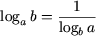
| (a 0, a ≠ 1, b 0, b ≠ 1). |
| (2) |
Используя свойства P4 и P5, легко получить следующие свойства
| 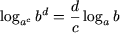
| (a 0, a ≠ 1, b 0, c ≠ 0), |
| (3) |
| 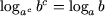
| (a 0, a ≠ 1, b 0, c ≠ 0), |
| (4) |
| 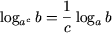
| (a 0, a ≠ 1, b 0, c ≠ 0), |
| (5) |
и, если в (5) c - четное число (c = 2n), имеет место
| 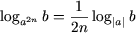
| (b 0, a ≠ 0, |a| ≠ 1). |
| (6) |
Перечислим и основные свойства логарифмической функции f(x) = loga x:
Область определения логарифмической функции есть множество положительных чисел.
Область значений логарифмической функции - множество действительных чисел.
При a 1 логарифмическая функция строго возрастает (0 x1 x2 loga x1 ax2), а при 0 a x1 x2 loga x1 loga x2).
loga 1 = 0 и loga a = 1 (a 0, a ≠ 1).
Если a 1, то логарифмическая функция отрицательна при x (0;1) и положительна при x (1;+), а если 0 a x (0;1) и отрицательна при x (1;+).
Если a 1, то логарифмическая функция выпукла вверх, а если a (0;1) - выпукла вниз.
Следующие утверждения (см., например, [1]) используются при решении логарифмических уравнений.
Утверждение 2. Уравнение loga f(x) = loga g(x) (a 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)
| 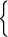
| f(x) = g(x), | | 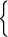
| f(x) = g(x), |
| f(x) 0, | g(x) 0. |
Утверждение 3. Уравнение logh(x) f(x) = logh(x) g(x) равносильно одной из систем
| 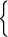
| f(x) = g(x), | | 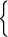
| f(x) = g(x), |
| h(x) 0, | h(x) 0, |
| h(x) ≠ 1, | h(x) ≠ 1, |
| f(x) 0, | g(x) 0. |
Нужно подчеркнуть, что в процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений (ОДЗ) исходного уравнения. Следовательно, могут появиться "чужие" решения или могут быть потеряны решения. Например, уравнения
f(x) = g(x) и loga f(x) = loga g(x)
или
loga [f(x)·g(x)] = b и loga f(x) + loga g(x) = b
вообще говоря, неравносильны (ОДЗ уравнений справа уже).
Следовательно, при решении логарифмических уравнений полезно использовать равносильные преобразования. В противном случае, проверка полученных решений является составной частью решения. Более того, необходимо учитывать и преобразования, которые могут привести к потере корней.
Задачи:
Решить уравнения:
a) log2 x = 3, b) log3 x = -1, c) 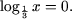
Решить уравнения
| a) log2(5 + 3log2(x - 3)) = 3, | c) log(x - 2)9 = 2, |
| b) 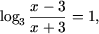 | d) log2x + 1(2x2 - 8x + 15) = 2. |
Решить уравнения
| a) log3x + log3(x + 3) = log3(x + 24), |
| b) log4(x2 - 4x + 1) - log4(x2 - 6x + 5) = -1/2 |
| c) log2x + log3x = 1, |
| d) 2log3(x - 2) + log3(x - 4)2 = 0, |
|
|
Решить уравнения
| a) lg2x - 3lgx + 2 = 0, | c) lg2100x + lg210x + lgx = 14, |
| b) 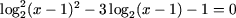 , , | d) 5lgx = 50 - xlg5. |
Решить уравнения
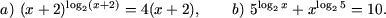
Решить уравнения
| a) 2x = 9 - log3x; |
| b) 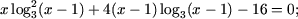 |
| c) log2(x2 + 1) - log2x = 2x - x2; |
| d) log5(x + 2) = 4 - x; |
| e) 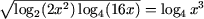 |
| f) |log2(3x - 1) - log23| = |log2(5 - 2x) - 1|; |
Решите уравнение: 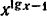 = 100.
= 100.
Решите уравнение: 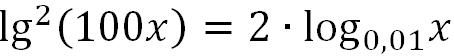 .
.
Решить уравнение: 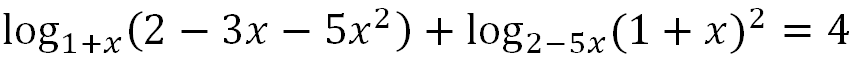
Решите уравнение: 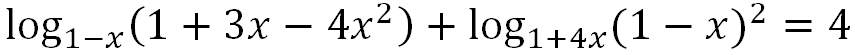 .
.
На перерыв.
а) Решите уравнение 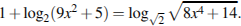
б) Найдите все корни этого уравнения, принадлежащие отрезку 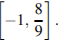
2