Файл к занятию 20.
Проверка домашнего задания
Задание 8. При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f0=170 Гц и определяется следующим выражением: f=f0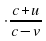 (Гц), где c — скорость распространения сигнала в среде (в м/с), а u=13 м/с и v=8 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 175 Гц? Ответ: 722
(Гц), где c — скорость распространения сигнала в среде (в м/с), а u=13 м/с и v=8 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 175 Гц? Ответ: 722
Задание 10. В ходе распада радиоактивного изотопа его масса уменьшается по закону
m = m0 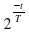 , где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 80 мг. Период его полураспада составляет 2 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг. Ответ: 8
, где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 80 мг. Период его полураспада составляет 2 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг. Ответ: 8
Дополнительно. В ходе распада радиоактивного изотопа его масса уменьшается по закону m = m0 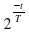 , где m0 (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа m0=200 мг. Период его полураспада T=3 мин. Через сколько минут масса изотопа будет равна 25 мг? Ответ: 9
, где m0 (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа m0=200 мг. Период его полураспада T=3 мин. Через сколько минут масса изотопа будет равна 25 мг? Ответ: 9
Решение заданий
Задание 1. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a (в км/ч2 ). Скорость v (в км/ч) вычисляется по формуле v=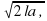 где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /ч2. Ответ: 5500
где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /ч2. Ответ: 5500
Задание 2. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=45 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние d2 от линзы до экрана — в пределах от 160 до 180 см. Изображение на экране будет четким, если выполнено соотношение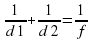 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Решение.
Поскольку f=45 имеем: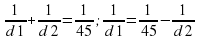
.
Из равенства видно, что наименьшему возможному значению d1 соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность 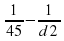 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 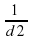 . Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=180,
. Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=180,
откуда 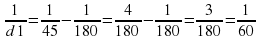 . Значит, d1=60 см
. Значит, d1=60 см
По условию лампочка должна находиться на расстоянии от 50 до 70 см от линзы. Найденное значение 60 см удовлетворяет условию. Ответ: 60.
Дополнительно. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=50 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 60 до 80 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 175 см. Изображение на экране будет четким, если выполнено соотношение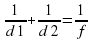 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Решение.
Так как f=50, то имеем: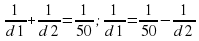
.
Из равенства видно, что наименьшему возможному значению d1 соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность 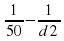 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 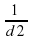 . Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=175,
. Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=175,
откуда 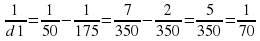 . Значит, d1=70 см
. Значит, d1=70 см
По условию лампочка должна находиться на расстоянии от 60 до 80 см от линзы. Найденное значение 70 см удовлетворяет условию. Ответ: 70.
Задание 3. Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону 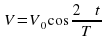 где t — время с момента начала колебаний, T = 2 с — период колебаний,
где t — время с момента начала колебаний, T = 2 с — период колебаний, 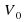 =1,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
=1,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле 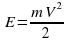 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Решение.
Найдем скорость груза через 56 секунд после начала колебаний. Для этого подставим значения 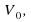 t, T в формулу для вычисления скорости:
t, T в формулу для вычисления скорости:
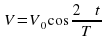 ;
;
V=1,6cos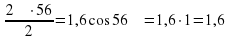
Найдем кинетическую энергию груза через 56 секунд после начала колебаний:
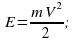 E =
E =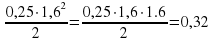 .
.
Ответ: 0,32
Задание 4. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону V=V0sin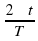 , где t ‐ время с момента начала колебаний, T = 16 с – период колебаний, v0=0,5м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E =
, где t ‐ время с момента начала колебаний, T = 16 с – период колебаний, v0=0,5м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E =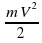 , где m‐ масса груза в килограммах, V ‐ скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях. (Ответ: 0,05)
, где m‐ масса груза в килограммах, V ‐ скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях. (Ответ: 0,05)
Задание 5. Два тела массой m=2 кг каждое, движутся с одинаковой скоростью V=10 м/с под углом 2 друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q=mV2sin2
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q=mV2sin2 . Под каким наименьшим углом
. Под каким наименьшим углом 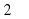 (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 100 джоулей?
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 100 джоулей?
Решение.
Задача сводится к решению неравенства Q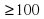 Дж на интервале 2
Дж на интервале 2
 (
(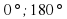 ) при заданных значениях массы тел m=2 кг и их скоростей V=10 м/с:
) при заданных значениях массы тел m=2 кг и их скоростей V=10 м/с:
mV2sin2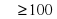 ;
;
200 sin2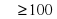 ;
;
sin2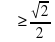 ;
;
Решение данного неравенства
sin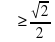 то sin
то sin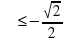
Так как 
 (
(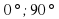 ) , то sin
) , то sin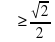 ,
,
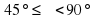
Следовательно, наименьший угол 2 =2
=2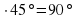
Ответ: 90.
Задание 6. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p1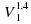 = p2
= p2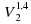 , где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 243,2 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 7,6
, где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 243,2 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 7,6
Дополнительно. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p1V1 1,4=p2V2 1,4, где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 9,2
Задание 7. Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела Р, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры: Р=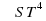 , где
, где 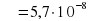 - постоянная, площадь S измеряется в квадратных метрах, а температура Т — в градусах Кельвина. Известно, что некоторая звезда имеет площадь S=
- постоянная, площадь S измеряется в квадратных метрах, а температура Т — в градусах Кельвина. Известно, что некоторая звезда имеет площадь S= 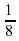 1
1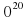 м2, а излучаемая ею мощность P=9,234
м2, а излучаемая ею мощность P=9,234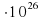 Вт. Определите температуру этой звезды. Приведите ответ в градусах Кельвина. Ответ: 6000.
Вт. Определите температуру этой звезды. Приведите ответ в градусах Кельвина. Ответ: 6000.
Задание 8. Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением A=  , где — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж. Ответ: 7.
, где — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж. Ответ: 7.
Задание 9. Водолазный колокол, содержащий в начальный момент времени υ=4 моля воздуха объeмом V1=14 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма V2. Работа, совершаемая водой при сжатии воздуха, определяется выражением A= (Дж), где
(Дж), где постоянная, а T=300 К — температура воздуха. Какой объeм V2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
постоянная, а T=300 К — температура воздуха. Какой объeм V2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
Ответ: 3,5.
Задание 10. Для обогрева помещения, температура в котором равна Tп=20 °C , через радиатор отопления, пропускают горячую воду температурой Tв=60 °C . Расход проходящей через трубу воды m=0,3 кг / с. Проходя по трубе расстояние x (м), вода охлаждается до температуры T, причeм x=α⋅ ⋅log2
⋅log2 (м), где с=4200
(м), где с=4200 – теплоeмкость воды,
– теплоeмкость воды,  – коэффициент теплообмена, а α =0,7 – постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м? Ответ: 30
– коэффициент теплообмена, а α =0,7 – постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м? Ответ: 30
Задание 11. Ёмкость высоковольтного конденсатора в телевизоре C=3⋅10− 6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R=2⋅106 Ом. Во время работы телевизора напряжение на конденсаторе U0=30 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t=αRClog2 (с), где α =1,4 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 25,2 секунды. Ответ дайте в кВ (киловольтах). Ответ: 3,75
(с), где α =1,4 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 25,2 секунды. Ответ дайте в кВ (киловольтах). Ответ: 3,75
Задание 12. В розетку электросети подключена электрическая духовка, сопротивление которой составляет R1 =72 Ом. Параллельно с ней в розетку предполагается подключить электрообогреватель, сопротивление которого R2 (в Ом).
При параллельном соединении двух электроприборов с сопротивлениями R1 и R2 их общее сопротивление вычисляется по формуле Rобщ = Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 8 Ом. Определите наименьшее возможное сопротивление электрообогревателя. Ответ дайте в омах. Ответ:9
Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 8 Ом. Определите наименьшее возможное сопротивление электрообогревателя. Ответ дайте в омах. Ответ:9
Дополнительно. Ёмкость высоковольтного конденсатора в телевизоре C=6⋅10− 6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R=8⋅106 Ом. Во время работы телевизора напряжение на конденсаторе U0=34 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t=αRClog2 (с), где α=0,8 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 76,8 секунды. Ответ дайте в кВ (киловольтах).
(с), где α=0,8 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 76,8 секунды. Ответ дайте в кВ (киловольтах).
Задание 13. Рейтинг R интернет-магазина вычисляется по формуле R= rпок -  ,
,
где m = ,
,  — средняя оценка магазина покупателями (от 0 до 1),
— средняя оценка магазина покупателями (от 0 до 1),  — оценка магазина экспертами (от 0 до 0,7) и К — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 26, их средняя оценка равна 0,68,а оценка экспертов равна 0,23.Ответ:0,63.
— оценка магазина экспертами (от 0 до 0,7) и К — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 26, их средняя оценка равна 0,68,а оценка экспертов равна 0,23.Ответ:0,63.
Задание 14. Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый показатель оценивается целыми числами от -2 до 2.
Аналитик, составляющий формулу, считает, что объективность публикаций ценится вдвое, а информативность — втрое дороже, чем оперативность. В результате, формула примет вид
R= . Каким должно быть число A, чтобы издание, у которого все показатели наибольшие, получило рейтинг 30? Ответ:0,4.
Задание 15.
На рисунке изображена схема моста. Вертикальные
пилоны связаны провисающей
цепью. Тросы, которые свисают с цепи и поддерживают
полотно моста, называются
вантами.
Введём систему координат:
ось Oy направим вертикально вверх вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано
на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой
y=0,0029x2−0,53x+28,
где x и y измеряются в метрах. Найдите длину ванты, расположенной
в 90 метрах от пилона. Ответ дайте в метрах. Ответ: 3,79


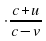
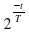
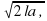 где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /ч2. Ответ: 5500
где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /ч2. Ответ: 5500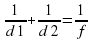 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. 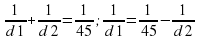
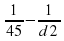 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 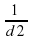 . Оно достигается при наибольшем возможном значении знаменателя
. Оно достигается при наибольшем возможном значении знаменателя 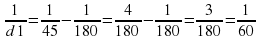
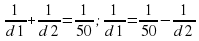
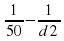 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 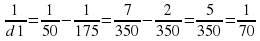
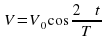 где
где 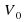 =1,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
=1,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле 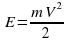 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.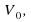
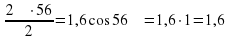
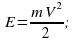
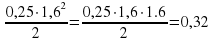 .
. 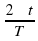
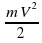 , где
, где  друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением 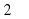 (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 100 джоулей?
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 100 джоулей?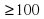
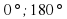 ) при заданных значениях массы тел
) при заданных значениях массы тел 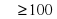
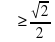
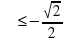
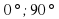 ) , то
) , то 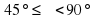
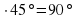
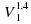
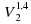
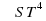 , где
, где 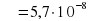 - постоянная, площадь S измеряется в квадратных метрах, а температура Т — в градусах Кельвина. Известно, что некоторая звезда имеет площадь S=
- постоянная, площадь S измеряется в квадратных метрах, а температура Т — в градусах Кельвина. Известно, что некоторая звезда имеет площадь S= 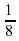 1
1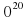 м2, а излучаемая ею мощность P=9,234
м2, а излучаемая ею мощность P=9,234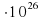 Вт. Определите температуру этой звезды. Приведите ответ в градусах Кельвина. Ответ: 6000.
Вт. Определите температуру этой звезды. Приведите ответ в градусах Кельвина. Ответ: 6000.