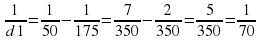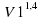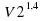Файл к занятию 19
Задание 1. Некоторая компания продает свою продукцию по цене p=400 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v=200 руб., постоянные расходы предприятия f=500000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле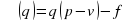 . Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб. Ответ: 7500
. Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб. Ответ: 7500
Задание 2. Зависимость объeма спроса q(единиц в месяц) на продукцию предприятия – монополиста от цены p (тыс. руб.) задаeтся формулой q=100-10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p)=qp. Определите наибольшую цену p, при которой месячная выручка r(p) составит 240 тыс. руб. Ответ приведите в тыс. руб. Ответ: 6.
Дополнительно. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q=130−10p. Выручка предприятия за месяц r (тыс. руб.) вычисляется по формуле r(p)=pq. Определите наибольшую цену p, при которой месячная выручка r(p) составит 420 тыс. руб. Ответ приведите в тыс. руб. Ответ: 7
Задание 3. Расстояние от наблюдателя, находящегося на небольшой высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле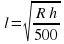 , где R=6400 км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 16 километров? Ответ выразите в метрах. Ответ: 20
, где R=6400 км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 16 километров? Ответ выразите в метрах. Ответ: 20
Задание 4. Наблюдатель находится на высоте h, выраженной в метрах. Расстояние
от наблюдателя до наблюдаемой им линии горизонта, выраженное
в километрах, вычисляется по формуле 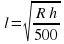 ,где R= 6400 км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 64 километра? Ответ дайте в метрах. Ответ: 64
,где R= 6400 км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 64 километра? Ответ дайте в метрах. Ответ: 64
Задание 5. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле 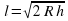 , где R=6400 км — радиус Земли. С какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах. Ответ: 0,08
, где R=6400 км — радиус Земли. С какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах. Ответ: 0,08
Задание 6. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+12t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров? Ответ: 0,8.
Задача 7.Высота над землёй подброшенного вверх мяча меняется по закону h(t)=2+12 t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров? Ответ: 1,6
Задание 8. В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t)=a t2+b t+H0, где H0=3 м — начальный уровень воды, a=1/768 м/мин 2 и b=− 1/8 м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах. Ответ: 48.
Дополнительно. В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t)=a t2+b t+H0, где H0=3 м — начальный уровень воды, a=1/588 м/мин 2 и b=− 1/7 м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах. Ответ: 42
Задание 9. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением T(t)=T0+bt+at2 , где t — время в минутах, Т0=1280 К, а= -10 К/мин2, b= 120К/мин. Известно, что при температуре нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах. Ответ: 4
Задание 10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора получена экспериментально: T=T0+b t+a t2, где t — время в минутах, T0=1450 К, a=− 30 К/мин 2, b=180 К/мин. Известно, что при температуре нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключить. Через сколько минут после начала работы нужно отключить прибор? Ответ: 1
Задание 11. Мяч бросили под углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле t=2v0sinα/g. При каком наименьшем значении угла α (в градусах) время полёта будет не меньше 3,2 секунды, если мяч бросают с начальной скоростью v0=32 м/с? Считайте, что ускорение свободного падения g=10 м/с2. Ответ: 30
Задание 12. Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой H= 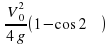 , где v0 =8 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с2). При каком наименьшем значении угла α (в градусах) мячик пролетит над стеной высотой 0,6 м на расстоянии 1 м? Ответ: 45.
, где v0 =8 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с2). При каком наименьшем значении угла α (в градусах) мячик пролетит над стеной высотой 0,6 м на расстоянии 1 м? Ответ: 45.
Задание 13. При сближении источника и приемника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приeмником, не совпадает с частотой исходного сигнала f0=130 Гц и определяется следующим выражением: f=f0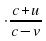 (Гц), где c — скорость распространения сигнал а в среде (в м/с), а u=16 м/с и v=15 м/с — скорости приeмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приeмнике f будет не менее 135 Гц? Ответ: 821.
(Гц), где c — скорость распространения сигнал а в среде (в м/с), а u=16 м/с и v=15 м/с — скорости приeмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приeмнике f будет не менее 135 Гц? Ответ: 821.
Задание 14. При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f0=170 Гц и определяется следующим выражением: : f=f0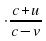 (Гц), где c — скорость распространения сигнала в среде (в м/с), а u=12 м/с и v=6 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 180 Гц?
(Гц), где c — скорость распространения сигнала в среде (в м/с), а u=12 м/с и v=6 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 180 Гц?
Задание 15. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 713 МГц. Скорость погружения батискафа, выражаемая в м/с, определяется по формуле v=c⋅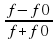 , где c=1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 12 м/с.
, где c=1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 12 м/с.
Задание 16. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 494 МГц. Скорость погружения батискафа v вычисляется по формуле v=c⋅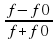 , где с =1500 м /с — скорость звука в воде, f0 — частота испускаемых импульсов, f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц,
, где с =1500 м /с — скорость звука в воде, f0 — частота испускаемых импульсов, f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц,
если скорость погружения батискафа равна 18 м/с.
Задание 17. В ходе распада радиоактивного изотопа его масса уменьшается по закону m = m0 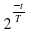 где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 96 мг. Период его полураспада составляет 3 мин. Найдите, через сколько минут масса изотопа будет равна 3 мг. Ответ: 15
где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 96 мг. Период его полураспада составляет 3 мин. Найдите, через сколько минут масса изотопа будет равна 3 мг. Ответ: 15
Задание 18. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=45 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние d2 от линзы до экрана — в пределах от 160 до 180 см. Изображение на экране будет четким, если выполнено соотношение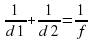 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Решение.
Поскольку f=45 имеем: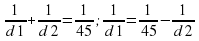
.
Из равенства видно, что наименьшему возможному значению d1 соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность 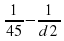 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 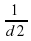 . Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=180,
. Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=180,
откуда 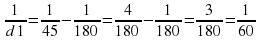 . Значит, d1=60 см
. Значит, d1=60 см
По условию лампочка должна находиться на расстоянии от 50 до 70 см от линзы. Найденное значение 60 см удовлетворяет условию. Ответ: 60.
Задание 19. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=50 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 60 до 80 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 175 см. Изображение на экране будет четким, если выполнено соотношение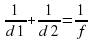 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Решение.
Так как f=50, то имеем: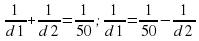
.
Из равенства видно, что наименьшему возможному значению d1 соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность 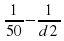 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 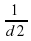 . Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=175,
. Оно достигается при наибольшем возможном значении знаменателя d2. Поэтому d2=175,
откуда 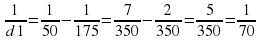 . Значит, d1=70 см
. Значит, d1=70 см
По условию лампочка должна находиться на расстоянии от 60 до 80 см от линзы. Найденное значение 70 см удовлетворяет условию. Ответ: 70.
Задание 20. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p1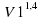 =p2
=p2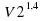 , где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах)
, где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах)
в начальном и конечном состояниях. Изначально объём газа равен 243,2 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах. Ответ: 7,6


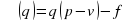 . Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб. Ответ: 7500
. Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб. Ответ: 7500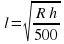 , где
, где 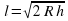 , где
, где 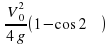 , где
, где 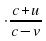
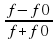
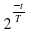 где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 96 мг. Период его полураспада составляет 3 мин. Найдите, через сколько минут масса изотопа будет равна 3 мг. Ответ: 15
где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 96 мг. Период его полураспада составляет 3 мин. Найдите, через сколько минут масса изотопа будет равна 3 мг. Ответ: 15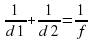 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. 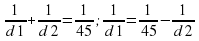
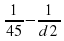 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого 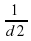 . Оно достигается при наибольшем возможном значении знаменателя
. Оно достигается при наибольшем возможном значении знаменателя 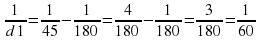
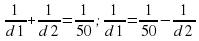
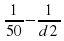 в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при неизменном уменьшаемом и наименьшем значении вычитаемого