Файл к занятию 22
Повторить теоретический материал:
Таблица производных
| f(x) | f`(x) |
| C=const | 0 |
| x | 1 |
| 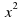
| 2x |
| 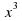
| 3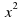 |
| 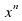
| n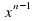 |
| 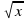
| 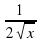
|
| 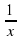
| 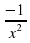
|
| sin x | cos x |
| cos x | -sin x |
| tg x | 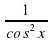
|
| ctg x | 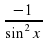
|
| 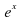
| 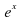
|
| ln x | 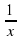
|
| 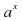
| 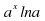
|
Правила вычисления производных.
Если у функций U и V существуют производные (V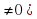 , то
, то
(U+V)`=U`+V`
(UV)`= U`V+V`U
(CU)`= CU`
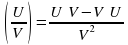
Производная сложной функции:
h`(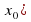 = g`(f(
= g`(f(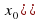 f
f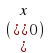
Достаточный признак возрастания (убывания) функции
1. Если f `(x)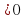 в каждой точке интервала (
в каждой точке интервала (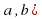 , то функция возрастает на (
, то функция возрастает на (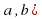 .
.
2. Если f `(x)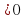 в каждой точке интервала (
в каждой точке интервала (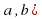 , то функция убывает на (
, то функция убывает на (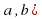 .
.
Достаточное условие экстремума
Если f `(x0)=0 и при переходе через точку x0 значение производной меняет знак с «+» на « - », то x0 является точкой максимума функции.
Если f `(x0)=0 и при переходе через точку x0 значение производной меняет знак с « - » на «+», то x0 является точкой минимума функции.
Задание 1. На рисунке изображен график производной функции f(x), определенной на интервале (-4;16). Найдите количество точек максимума функции f(x) на отрезке 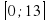 . Ответ: 1
. Ответ: 1

Задание 2. На рисунке изображен график производной функции f(x), определенной на интервале (-2;21). Найдите количество точек максимума функции f(x) на отрезке 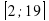 . Ответ:2
. Ответ:2

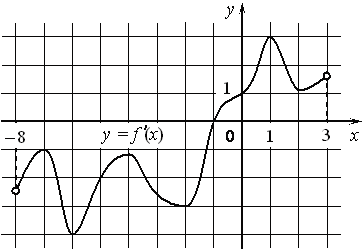
Задание 3.На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 3). В какой точке отрезка [− 6; −1] функция f(x) принимает наименьшее значение? Ответ: -1
Дополнительно. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 6; 5). В какой точке трезка [− 5; −1] функция f(x) принимает наименьшее значение? Ответ: -5
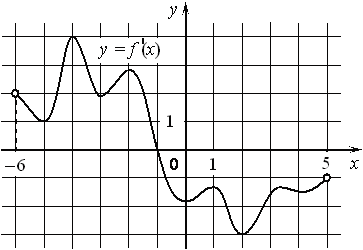
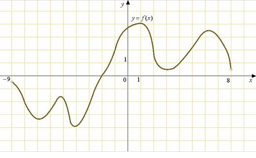
Задание 4. На рисунке изображен график функции y=f(x), определенной на интервале(−6; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = -6 или совпадает с ней.
Ответ: 7.
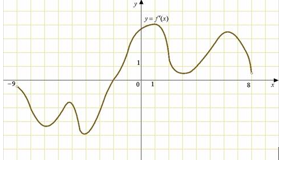
Задание 5. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 10). Найдите количество точек минимума функции f(x) на отрезке [−3; 8].

Решение. Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−3; 8] функция имеет одну точку минимума x = 4. Значит, ответ 1. Ответ: 1.
Алгоритм нахождения точек экстремума
Найти область определения функции.
Найти производную функции f '(x)
Найти точки, в которых f '(x) = 0.
Отметить на числовой прямой область определения функции и все нули производной.
Определить знак производной для каждого промежутка. (Для этого подставляем "удобное" значение x из этого промежутка в f '(x)).
Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере (max или min) в каждой из критических точек.
Задание 1. Найдите точку максимума функции у = х3–5х2+7х–5. Ответ: 1
Дополнительно. Найдите точку максимума функции y= 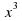 +6,5
+6,5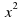 -30x+23. Ответ: -6.
-30x+23. Ответ: -6.
Задание 2. Найдите точку минимума функции у = х3+5х2+7х–5.Ответ: 2
Ответ: –1
Дополнительно. Найдите точку минимума функции y=х3−4х2+4x+17. Ответ: 2
Задание 3. Найдите точку максимума функции y = ln(x+9)−10x+7. Ответ: -8,9
Задание 4. Найдите точку минимума функции y = 4х- ln(x+11)+12. Ответ: -10,75
Дополнительно. Найдите точку минимума функции y=1,5x2 −30x+48⋅lnx+4.
Задание 5. Найдите точку минимума функции y = 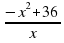 . Ответ: -6
. Ответ: -6
Дополнительно: Найдите точку максимума функции y = 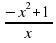 .
.
Задание 6. Найдите точку минимума функции y=10x-10ln(x+7)+5 . Ответ: -6
Задание 7. Найдите точку максимума функции y= (x+16)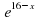 . Ответ: -15
. Ответ: -15
Наибольшее и наименьшее значение функции на отрезке
Непрерывная на отрезке функция достигает своего наименьшего и наибольшего значений либо во внутренних точках промежутка, либо на его концах. Поэтому для решения задач этого типа достаточно определить значения функции в точках экстремума и сравнить их с её значениями на концах отрезка. Выявлять тип экстремума необязательно.
Алгоритм нахождения наибольшего и наименьшего значение функции на отрезке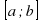
Найти производную функции f '(x).
Найти точки, в которых f '(x) = 0. Проверить принадлежность этих точек отрезку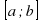
Найти значение функции на концах отрезка и в данных точках.
Выбрать из полученных значений наибольшее или наименьшее.
Задание 8. Найдите наименьшее значение функции y= 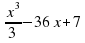 на отрезке
на отрезке 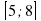 . Ответ: -137
. Ответ: -137
Задание 9. Найдите наибольшее значение функции у= х3-6,5х2+14х-14 на отрезке[− 4; 3]. Ответ: -3,5
Задание 10. Найдите наибольшее значение функции y= (x+2)2(x+8)-7 на отрезке 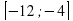 . Ответ: 25
. Ответ: 25
Задание 11. Найдите наибольшее значение функции y=х5 +20х3−65x на отрезке [− 4; 0]. Ответ: 44
|
|
| Задание 12. Найдите наибольшее значение функции y=10⋅ln(x+8)−10x−18 на
отрезке [− 7,5 ; 0]. Ответ: 52 |
Дополнительно. Найдите наибольшее значение функции y=12⋅ln(x+2)−12x+7 на отрезке [− 1,5 ; 0]. Ответ: 19
Задание 13. Найдите наибольшее значение функции y =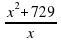 на отрезке [−38; -3].Ответ: -54
на отрезке [−38; -3].Ответ: -54


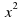
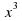
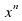
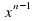
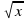
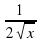
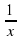
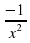
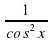
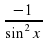
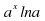
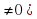
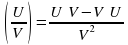
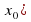 =
= 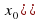
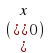
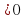 в каждой точке интервала (
в каждой точке интервала (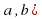 , то функция возрастает на (
, то функция возрастает на (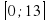 . Ответ: 1
. Ответ: 1
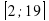 . Ответ:2
. Ответ:2

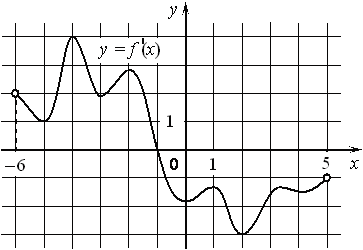


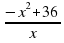 . Ответ: -6
. Ответ: -6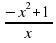 .
. 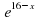 . Ответ: -15
. Ответ: -15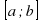
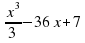 на отрезке
на отрезке 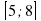 . Ответ: -137
. Ответ: -137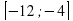 . Ответ: 25
. Ответ: 25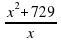 на отрезке [−38; -3].Ответ: -54
на отрезке [−38; -3].Ответ: -54