Файл к занятию 11
Многогранники
Призма
Призмой называется многогранник, у которого две грани-равные n-угольники, а остальные n граней — параллелограммы. Равные n-угольники называются основаниями, параллелограммы - боковыми гранями призмы. Боковые ребра призмы равны и параллельны.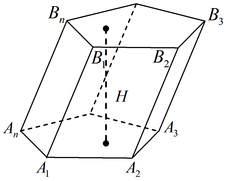
Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы. Поверхность призмы состоит из оснований и боковой поверхности призмы. Боковая поверхность призмы состоит из параллелограммов.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. В противном случае призма называется наклонной.
У прямой призмы боковые грани – прямоугольники.
Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если она прямая, и ее основания — правильные многоугольники.
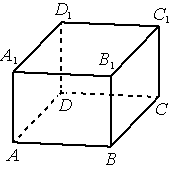
Параллелепипед
Параллелепипедом называется призма, основанием которой является параллелограмм.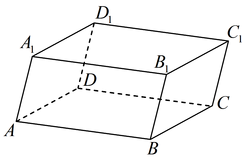
Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда все грани — параллелограммы.
Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда.
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.
Длины не параллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три линейных размера.
Свойства параллелепипеда:
Противоположные грани параллелепипеда равны и параллельны.
Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Боковые грани прямого параллелепипеда — прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Задание 1. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=16, A1B1=2, A1D1=8. Найдите длину диагонали AC1. Ответ:18
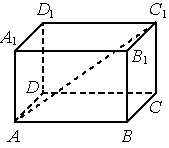
Задание 2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=21, AD=20, AA1=23. Найдите площадь сечения, проходящего через вершины A, A1 и C. Ответ: 667
Пирамида
Пирамида (n-угольная)-это многогранник, у которого одна грань- какой-нибудь n –угольник, а остальные n граней- треугольники с общей вершиной. n -угольник называется основанием, треугольники с общей вершиной- боковыми гранями, их общая вершина- вершина пирамиды.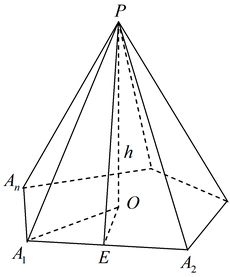
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Тетраэдр — это пирамида, в основании которой лежит треугольник.
Треугольники, из которых состоит тетраэдр, называются его гранями, их стороны — ребрами, а вершины — вершинами тетраэдра. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. Обычно выделяют одну из граней тетраэдра и называют ее основанием, а остальные грани называют боковыми гранями.
Правильным тетраэдром называют тетраэдр, у которого все ребра равны.
Правильной пирамидой называется такая пирамида, основание которой— правильный многоугольник, а все боковые ребра равны между собой. Основание высоты правильной пирамиды совпадает с центром основания. Прямая, содержащая высоту правильной пирамиды, называется ее осью.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Свойства правильной пирамиды:
Боковые ребра пирамиды равны.
Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.
Вершина пирамиды проектируется в центр окружности, описанной около основания пирамиды.
Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны, а высота пирамиды лежит внутри пирамиды.
Все двугранные углы при основании пирамиды равны.
Вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды.
Помним:
Если боковые ребра пирамиды равны между собой, то в основании лежит правильный многоугольник, вокруг которого можно описать окружность, а вершина пирамиды проецируется в центр этой окружности.
Если двугранные углы при основании пирамиды равны между собой, то в основании пирамиды лежит многоугольник, в который можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.
Задание 3. В правильной четырёхугольной пирамиде SABCD с вершиной S точка O – центр основания, SO=35, SD=37.Найдите длину отрезка BD.Ответ:24
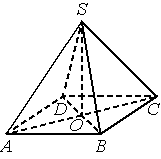
Задание 4. В правильной четырёхугольной пирамиде SABCD
с вершиной S точка O — центр основания, SD=26, AC=20. Найдите длину отрезка SO. Ответ:24

Задание 5. В правильной треугольной пирамиде боковое ребро
равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды. Ответ: 3,5
Площадь поверхности и объём призмы
Пусть H — высота призмы, A1B1 — боковое ребро призмы, Росн — периметр основания призмы, Sосн площадь основания призмы, Sбок— площадь боковой поверхности призмы, Sполн — площадь полной поверхности призмы, V - объем призмы, P — периметр перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
— периметр перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Sбок = P
 A1B1
A1B1
Sполн = 2Sосн + Sбок
V= Sосн 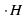
Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований:
Sбок = Росн 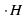
V= Sосн 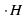
Задание 6. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. Ответ:248
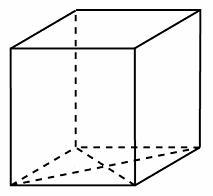
Задание 7. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы. Ответ:42
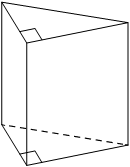
Задание 8. Два ребра прямоугольного параллелепипеда равны 8 и 2,
а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда. Ответ: 212
Пусть H — высота пирамиды, Росн — периметр основания пирамиды, Sосн — площадь основания пирамиды, Sбок — площадь боковой поверхности пирамиды, Sполн — площадь полной поверхности пирамиды, V — объем пирамиды. Тогда имеют место следующие соотношения:
Sполн = Sосн + Sбок
V= 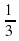 Sосн
Sосн 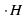
Если все двугранные углы при основании пирамиды равны  , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны hбок, то
, а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны hбок, то
Sбок = 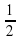 Росн
Росн  hбок ; Sбок =
hбок ; Sбок = 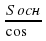
Для правильной пирамиды: Sбок = 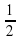 Росн
Росн  hбок
hбок
Задание 9. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. Ответ: 340
Задание 10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём. В ответ запишите объем, деленный на 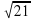 . Ответ: 14
. Ответ: 14
Задание 11. Найдите объем правильной треугольной пирамиды, сторона основания которой равна 3, а высота равна 6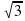 . Ответ:13,5
. Ответ:13,5
Задание 12. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды. Ответ:13

Задание 13. Сторона основания правильной шестиугольной пирамиды равна 10, боковое ребро равно 20. Найдите объем пирамиды. Ответ:1500
| Дополнительно: Задание 1. В правильной шестиугольной пирамиде боковое ребро равно 6,5, а сторона основания равна 2,5. Найдите высоту пирамиды. Ответ: 6 Задание 2.Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 20. Найдите площадь боковой поверхности этой пирамиды. Ответ:1152
| 
|
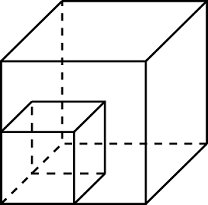
Задание 14. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:108
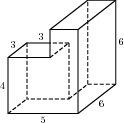
Задание 15. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ: 14
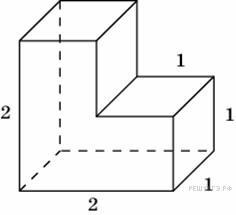
Задание 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ: 132

Задание 17 . Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в два раза? Во сколько раз увеличится объем? Ответ:4
Задание 18. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза? Ответ: 8
Задание 19. Пирамида Хефрена имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 210 м, а высота — 136 м. Сторона основания точной музейной копии этой пирамиды равна 105 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
Задание 20. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Ответ: 8
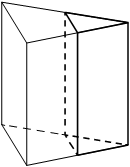
Задание 21. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7,5. Найдите объем исходной призмы. Ответ: 30
Задание 22. Площадь поверхности правильной треугольной призмы равна 12. Какой будет площадь поверхности призмы, если все ее ребра увеличить в шесть раз? Ответ: 432
Задание 23. Площадь боковой поверхности треугольной призмы равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы. Ответ: 37,5
Задание 24. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы. Ответ: 74











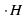

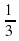
 , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны 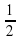 Росн
Росн 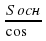
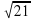 . Ответ: 14
. Ответ: 14
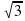 . Ответ:13,5
. Ответ:13,5