Файл к занятию 10.
Единичная окружность. Синус. Косинус. Тангенс. Котангенс.
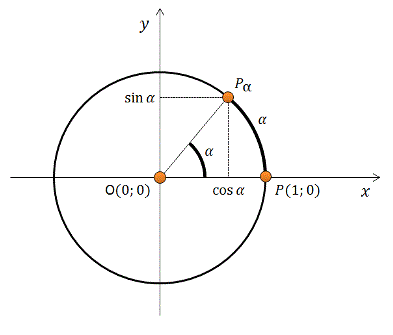 cos
cos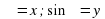
Зависимость между тригонометрическими функциями одного аргумента
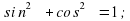
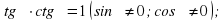
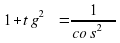
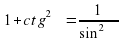
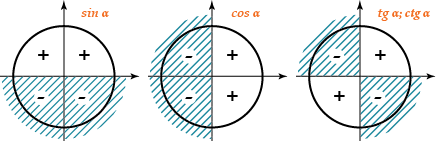 Формулы сложения
Формулы сложения
 ;
;
 ;
;
 ;
;
 .
.
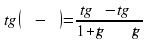 ;
;
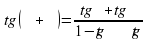 .
.
Формулы приведения Все формулы приведения получаются из соответствующих формул сложения.
Применение формул приведения можно свести к использованию правила:
Правило названий: если аргумент приводимой функции имеет вид ( 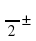
 ) или
) или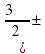
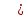 , то функция меняется на сходственную(на кофункцию) , если аргумент приводимой функции имеет вид
, то функция меняется на сходственную(на кофункцию) , если аргумент приводимой функции имеет вид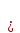
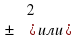
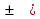 , то функция названия не меняет.
, то функция названия не меняет.
Правило знака: определяется координатная четверть, в которой лежит аргумент приводимой функции, в предположении, что  — острый угол, и определяется знак приводимой функции в этой четверти. ( Т.е. в правой части формулы ставится тот знак, который имеет значение выражения в левой части)
— острый угол, и определяется знак приводимой функции в этой четверти. ( Т.е. в правой части формулы ставится тот знак, который имеет значение выражения в левой части)
Формулы двойного аргумента (формулы двойного угла )
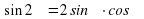 =
= 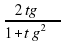
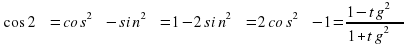
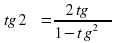 ;
;
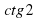 =
=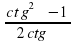
Свойства основных тригонометрических функций
Функции sinx, tgx, ctgx являются нечетными функциями, а cosx — четной:
sin (-x)= - sin x;
cos(-x) = cos x;
tg (-x) = - tg x;
ctg(-x) = - ctgx.
Период для функций sin x и cos x есть 2 ; для функций tg x и ctg x :
; для функций tg x и ctg x :  .
.
Задание 1. Найдите cosα , если sin α = 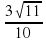 и α ∈ (π/2; π) . Ответ: -0,1
и α ∈ (π/2; π) . Ответ: -0,1
Задание 2. Найдите sinα , если cos α = 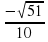 и α ∈ (π; 3π/2) . Ответ: -0,7
и α ∈ (π; 3π/2) . Ответ: -0,7
Задание 3. Найдите tgα , если cos α = 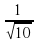 и α ∈ (3π/2; 2π). Ответ: −3.
и α ∈ (3π/2; 2π). Ответ: −3.
Задание 4. Найдите tgα , если sin α = 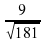 и α ∈ (0; π/2) . Ответ: 0,9.
и α ∈ (0; π/2) . Ответ: 0,9.
Задание 5. Найдите значение выражения 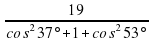 . Ответ: 9,5
. Ответ: 9,5
Задание 6. Найдите значение выражения 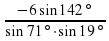 . Ответ:-12
. Ответ:-12
Задание7. Найдите значение выражения 46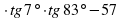 .Ответ:-11
.Ответ:-11
Задание 8.
1. Найдите значение выражения 7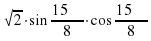 . Ответ: -3,5
. Ответ: -3,5
2. Найдите значение выражения 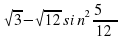 . Ответ: -1,5
. Ответ: -1,5
Самостоятельная работа
Задание 1. Найдите cosα , если sin α =- 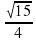 и 270°x360° . Ответ: 0,25
и 270°x360° . Ответ: 0,25
Задание 2. Найдите tgα , если sin α = 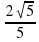 и α ∈ (π/2; π) . Ответ:-2
и α ∈ (π/2; π) . Ответ:-2
Задание 3. Найдите значение выражения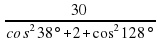 . Ответ: 10
. Ответ: 10
Задание 4. Найдите значение выражения 2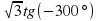 . Ответ:6
. Ответ:6
Задание 5. Найдите значение выражения 14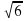
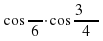 . Ответ:-21
. Ответ:-21
Задание 6. Найдите значение выражения 10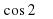 , если
, если 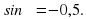 Ответ:5
Ответ:5
Арксинус, арккосинус, арктангенс числа.
Пусть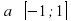 . Арксинусом числа
. Арксинусом числа 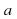 называется угол
называется угол  такой, что
такой, что 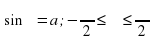 .
.
Например:;; ;
; arcsin
arcsin ; arcsin; arcsin
; arcsin; arcsin  ; arcsin(-1)
; arcsin(-1) .
.
Пусть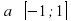 . Арккосинусом числа
. Арккосинусом числа 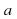 называется угол
называется угол  такой, что
такой, что  .
.
Например:;= ;
;
Пусть  Арктангенсом числа
Арктангенсом числа 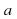 называется угол
называется угол  такой, что
такой, что 

Пусть  Арккотангенсом числа
Арккотангенсом числа 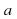 называется угол
называется угол  такой, что
такой, что 

Например:
Решение тригонометрических уравнений
Частные случаи:

 Z
Z
 Z
Z
 Z
Z


 Z
Z


 Z
Z


 Z
Z
Решение уравнения

Обычная форма записи решения
Помним, если  то уравнение
то уравнение  не имеет корней.
не имеет корней.
Задание 9.
1) Решите уравнение  .
.
2)укажите корни уравнения, принадлежащие отрезку [ -π ; 5π/2].
Ответ: 1)
2)
Решение уравнения

Обычная форма записи решения
Помним, если  то уравнение
то уравнение  не имеет корней.
не имеет корней.
Задание 10.
1) Решите уравнение Cos x=  ;
;
2) найдите его корни на промежутке 
Ответ: 1)
2)
Задание 11.
1) Решите уравнение: cos ( – x) =
– x) =  ;
;
2) укажите корни, принадлежащие отрезку 
Ответ: 1)
2)
Решение уравнения 
Обычная форма записи решения

Решение уравнения 
Обычная форма записи решения

Задание 12.
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку [π ; 7π/2].
Ответ: 1)
2)
Задание 13.
а) Решите уравнение  =1
=1
б) Найдите все корни этого уравнения, принадлежащие отрезку [0 ; π/4].
Ответ: 1) ;
; ;
;
2)



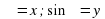
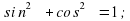
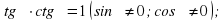
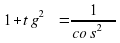
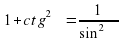
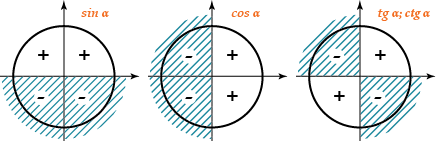 Формулы сложения
Формулы сложения ;
; ;
; ;
; .
.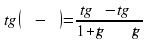 ;
;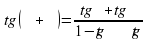 .
.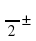
 ) или
) или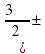
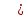 , то функция меняется на сходственную(на кофункцию) , если аргумент приводимой функции имеет вид
, то функция меняется на сходственную(на кофункцию) , если аргумент приводимой функции имеет вид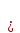
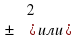
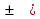 , то функция названия не меняет.
, то функция названия не меняет.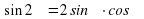 =
= 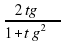
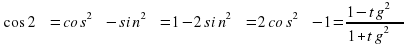
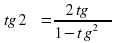
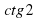
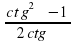
 ; для функций
; для функций 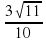
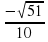
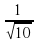
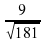
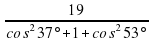 . Ответ: 9,5
. Ответ: 9,5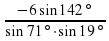 . Ответ:-12
. Ответ:-12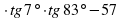 .Ответ:-11
.Ответ:-11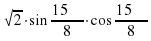 . Ответ:
. Ответ: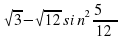 . Ответ: -1,5
. Ответ: -1,5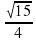
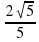
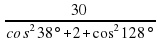 . Ответ: 10
. Ответ: 10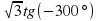 . Ответ:6
. Ответ:6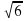
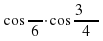 . Ответ:-21
. Ответ:-21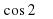 , если
, если 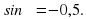 Ответ:5
Ответ:5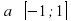 . Арксинусом числа
. Арксинусом числа 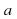 называется угол
называется угол 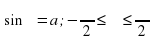 .
.