Файл к занятию 7
Числа и вычисления. Степени и корни.
Проверка домашнего задания.
Задание 8. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 15. Найдите площадь закрашенной фигуры. Ответ: 120

Задание 9. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры. Ответ:3

Числа и вычисления
Задание 1. Найдите значение выражения 7 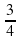 :
: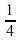 . Ответ: 31.
. Ответ: 31.
Задание 2. Найдите значение выражения 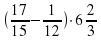 . Ответ: 7
. Ответ: 7
Задание 3. Найдите значение выражения (72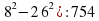 . Ответ:702
. Ответ:702
Задание 4. Найдите значение выражения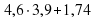 . Ответ: 19,68
. Ответ: 19,68
Свойства степени с рациональным показателем
Пусть дано положительное число a и произвольное рациональное число n. Число 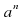 называется степенью, число a — основанием степени, число n — показателем степени. По определению полагают:
называется степенью, число a — основанием степени, число n — показателем степени. По определению полагают:
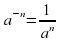 ;
; 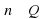
Если 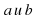 и — положительные числа,
и — положительные числа, 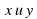 — любые рациональные числа, то справедливы следующие свойства:
— любые рациональные числа, то справедливы следующие свойства:
Задание 5. Найдите значение выражения (54)6:522. Ответ: 25
Задание 6. Найдите значение выражения (7х3)2:(7х6). Ответ: 7
Задание 7. Найдите значение выражения 20− 3,9⋅52,9:4− 4,9. Решение:
Запишем выражение в виде дроби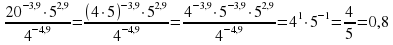 . Ответ: 0,8
. Ответ: 0,8
Задание 8. Найдите значение выражения 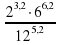 . Ответ:1,5
. Ответ:1,5
Задание 9. Найдите значение выражения 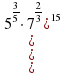 . Ответ:7
. Ответ:7
Задание 10. Найдите значение выражения 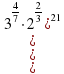 .Ответ:4
.Ответ:4
Задание 11. Найдите значение выражения 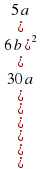 . Ответ: 5.
. Ответ: 5.
Помним: Если m — целое, а n — натуральное число и n ≥ 2, то 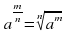 .
.
Задание 12. Найдите значение выражения 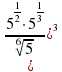 .Ответ: 25
.Ответ: 25
Задание 13. Найдите значение выражения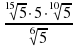 . Ответ:5
. Ответ:5
Решение: Заменим корни степенью числа 5: 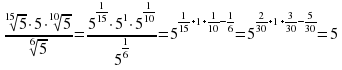
Задание 14. Найдите значение выражения 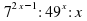 при x=
при x=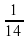 . Ответ:2
. Ответ:2
Степень с действительным показателем
Пусть дано положительное число 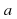 и произвольное действительное число
и произвольное действительное число 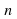 . При положительном основании понятие степени определено для любого рационального и для любого иррационального показателя, т.е. для любого действительного показателя. При этом все действия со степенями с произвольными действительными показателями обладают теми же свойствами, что и действия со степенями с рациональными показателями.
. При положительном основании понятие степени определено для любого рационального и для любого иррационального показателя, т.е. для любого действительного показателя. При этом все действия со степенями с произвольными действительными показателями обладают теми же свойствами, что и действия со степенями с рациональными показателями.
Помним: Если m — целое, а n — натуральное число и n ≥ 2, то 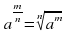 .
.
Задание 15. Найдите значение выражения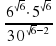 .Ответ: 900
.Ответ: 900
Задание 16. Найдите значение выражения 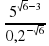 . Ответ:0,008
. Ответ:0,008
Корень n-ной степени
Пусть 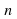 — натуральное число, неравное единице. Если
— натуральное число, неравное единице. Если 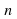 — четно, то арифметическим корнем
— четно, то арифметическим корнем 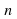 -ной степени из неотрицательного числа
-ной степени из неотрицательного числа 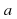 называется такое неотрицательное число,
называется такое неотрицательное число,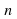 -ная степень которого равна
-ная степень которого равна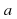 . Если
. Если 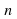 — нечетно, то арифметическим корнем
— нечетно, то арифметическим корнем 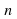 -ной степени из числа
-ной степени из числа 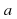 называется такое число,
называется такое число,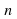 -ная степень которого равна
-ная степень которого равна 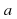 .
.
По определению: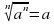 .
.
Свойства арифметического квадратного корня:
Квадратный корень из произведения неотрицательных чисел равен произведению квадратных корней из этих чисел. Т.е. при любых значениях 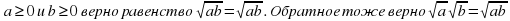 .
.
Квадратный корень из дроби с неотрицательным числителем и положительным знаменателем равен частному от деления квадратного корня из числителя на квадратный корень из знаменателя. Т.е. при любых значениях 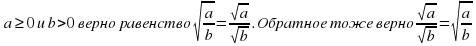 .
.
Задание 17. Вычислите значение числового выражения:
1) ; Ответ: 96
; Ответ: 96
2)  . Ответ:6
. Ответ:6
3)132
4)  . Ответ: 1056
. Ответ: 1056
Задание 18. Вычислите значение числового выражения:
1)  . Ответ: 2
. Ответ: 2
2) . Ответ:4
. Ответ:4
3 ) . Ответ: 5
. Ответ: 5
4). Ответ: 3
Задание 19. Найдите значение выражения . Ответ: 3
Помним : (
Задание 20. Найдите значение выражения:
1) (  -
-  ). Ответ: 6
). Ответ: 6
2) (  -
-  ). Ответ:21
). Ответ:21
3) (  -
-  ). Ответ:11
). Ответ:11
Задание 21. Найдите значение выражения:
1) . Ответ:-18
. Ответ:-18
2). Ответ:7
3). Ответ: -4
При любом значении 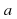 имеет место равенство
имеет место равенство 
Задание 22. Преобразовать выражение  при
при
1)р ≥-9. Ответ: р+9
2) р
Задание 23. Преобразовать выражение  при а
при а
Задание 24.Найдите значение выражения  при
при  . Ответ: 2
. Ответ: 2
Задание 25. Найдите значение выражения .Ответ: -2
Задание 26. Найдите значение выражения  .
.
Решение: Возведем числитель в квадрат и раскроем скобки: = = = 0,2. Ответ: 0,2
= = = 0,2. Ответ: 0,2
Задание 27. Освободитесь от иррациональности в знаменателе дроби:
1) 
2)
3)
Если a и b — неотрицательные числа, n и k — натуральные числа, отличные от единицы, m — целое число, то имеют место следующие соотношения:
Задание 28. Найдите значение выражения  при
при  .
.
Решение:
Воспользуемся свойствами корня . Ответ:9
. Ответ:9
Задание 29. Найдите значение выражения при  . Ответ: 4
. Ответ: 4
Задание 30. Найдите значение выражения:
.
Решение: Выделим полный квадрат под корнем и воспользуемся формулой
=
Аналогично выполним преобразование под вторым корнем:
= .
.
= . Ответ: 3
.
. Ответ запишите в виде десятичной дроби.




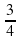 :
: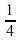 . Ответ: 31.
. Ответ: 31.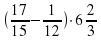 . Ответ: 7
. Ответ: 7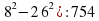 . Ответ:702
. Ответ:702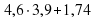 . Ответ: 19,68
. Ответ: 19,68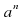 называется степенью, число
называется степенью, число 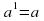
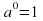
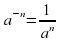
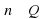
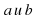 и — положительные числа,
и — положительные числа, 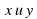 — любые рациональные числа, то справедливы следующие свойства:
— любые рациональные числа, то справедливы следующие свойства: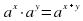
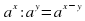
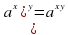
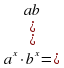
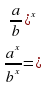
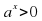
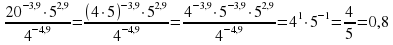 . Ответ: 0,8
. Ответ: 0,8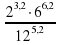 . Ответ:1,5
. Ответ:1,5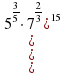 . Ответ:7
. Ответ:7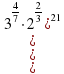
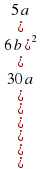 . Ответ: 5.
. Ответ: 5.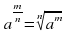 .
.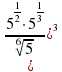 .Ответ: 25
.Ответ: 25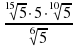 . Ответ:5
. Ответ:5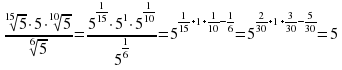
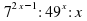 при
при 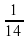 . Ответ:2
. Ответ:2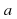 и произвольное действительное число
и произвольное действительное число 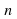 . При положительном основании понятие степени определено для любого рационального и для любого иррационального показателя, т.е. для любого действительного показателя. При этом все действия со степенями с произвольными действительными показателями обладают теми же свойствами, что и действия со степенями с рациональными показателями.
. При положительном основании понятие степени определено для любого рационального и для любого иррационального показателя, т.е. для любого действительного показателя. При этом все действия со степенями с произвольными действительными показателями обладают теми же свойствами, что и действия со степенями с рациональными показателями. 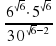 .Ответ: 900
.Ответ: 900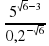 . Ответ:0,008
. Ответ:0,008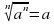 .
.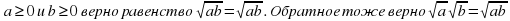 .
.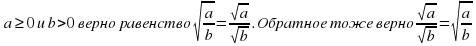 .
.