Разрезания. Замощения. Раскраски.

Раскраски. Разрезания. Замощения.

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абул-Вефа, знаменитого персидского астронома Х века, жившего в Багдаде. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них той или иной новой фигуры лишь в начале XX века. Одним из основоположников этого увлекательного раздела геометрии был знаменитый составитель головоломок Генри Э. Дьюдени. Особенно большое число существовавших ранее рекордов по разрезанию фигур побил эксперт австралийского патентного бюро Гарри Линдгрен. Он является ведущим специалистом в области разрезания фигур.

В наши дни любители головоломок увлекаются решением задач на разрезание прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берется за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Поскольку здесь не требуется глубокое знание геометрии, то любители иногда могут даже превзойти профессионалов-математиков.

Чтобы доказать, что решение задачи на разрезание какой-нибудь фигуры на части возможно, достаточно предоставить какой-нибудь способ разрезания. Найти все решения, то есть все способы разрезания, немного труднее. А доказать, что разрезание невозможно, уже достаточно трудно. Сделать это в некоторых случаях нам помогает раскраска фигуры.

Задача 1:  Взяли квадрат клетчатой бумаги размером 8×8, отрезали от него две клетки (левую нижнюю и правую верхнюю). Можно ли полученную фигуру полностью покрыть «доминошками» — прямоугольниками 1× 2?

Задача 2. Можно ли выложить шахматную доску тридцатью двумя доминошками так, чтобы 17 из них были расположены горизонтально, а 15 – вертикально?

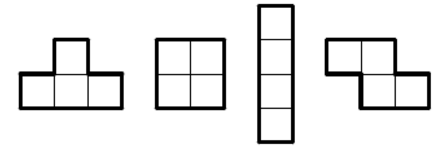
Задача 3: Можно ли разрезать квадрат клетчатой бумаги размером

4× 4 на один пьедестал, один квадрат, один столбик и один зигзаг?

Задача 4: Можно ли выложить квадрат 8 × 8, используя 15 прямоугольников 1 × 4 и один уголок вида ?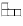

Задача 5: Можно ли выложить прямоугольник 6 × 10 прямоугольниками 1 × 4?

Задача 6: Можно ли сложить квадрат 6 × 6 с помощью 11 прямоугольников 1 × 3 и одного уголка вида ?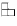

Задача 7: На каждой клетке доски 5 × 5 сидит жук. В некоторый момент времени все жуки взлетают и приземляются на соседние по стороне клетки. Докажите, что при этом окажется хотя бы одна пустая клетка.

Задача 8: Из доски 8 × 8 вырезали угловую клетку. Можно ли оставшуюся часть разрезать на прямоугольники 3 × 1?

Задача 9: Фигура «верблюд» ходит по шахматной доске ходом типа (1, 3). Можно ли пройти ходом «верблюда» с произвольного поля на соседнее?

Задача 10: Можно ли доску размером 10 × 10 покрыть фигурами вида ?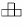

Задача 11: Дана доска 12 × 12. В левом нижнем углу стоят 9 шашек, образуя квадрат 3 × 3. За один ход можно выбрать какие-то две шашки и переставить одну из них симметрично относительно другой (не выходя при этом за пределы доски). Можно ли за несколько ходов переместить эти шашки так, чтоб они образовали квадрат 3 × 3 в правом нижнем углу?

Задача 12: В каждой клетке квадрата 9 × 9 сидит жук. По команде каждый жук перелетает на одну из соседних по диагонали клеток. Доказать, что по крайней мере 9 клеток после этого окажутся свободными.

Задача 13: Замок имеет форму правильного треугольника, разделенного на 25 маленьких залов той же формы. В каждой стене между залами проделана дверь. Путник ходит по замку, не посещая более одного раза ни один из залов. Найти наибольшее число залов, которое ему удастся посетить.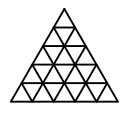

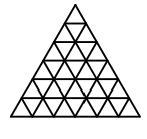
Задача 14: На какое наибольшее количество ромбов можно разрезать равносторонний треугольник, разбитый на 36 равносторонних треугольников?

Задача 15. В квадрате 7×7 клеток размещено 16 плиток размером 1×3 и одна плитка 1×1. Докажите, что плитка 1×1 либо лежит в центре, либо примыкает к границам квадрата.

Задача 16. В левый нижний угол шахматной доски 8×8 поставлено в форме квадрата 3×3 девять фишек. Фишка может прыгать на свободное поле через рядом стоящую фишку, то есть симметрично отражаться относительно её центра (прыгать можно по вертикали, горизонтали и диагонали). Можно ли за некоторое количество таких ходов поставить все фишки вновь в форме квадрата 3×3, но в другом углу:

а) левом верхнем,    б) правом верхнем?