Геометрические неравенства.
При изучении математики ученикам часто приходится сталкиваться с решением неравенств. Одними из наиболее сложных видов неравенств являются геометрические. В школе на их решение отводится не достаточное количество времени, поэтому при работе с подобными неравенствами у учеников возникают трудности. Однако на вступительных экзаменах в ВУЗы и на математических олимпиадах такого рода задания можно встретить достаточно часто. Рассмотрим некоторые из них.
Неравенство треугольника
Теорема (неравенство треугольника):
Каждая сторона треугольника меньше суммы двух других его сторон.
Замечание. Иногда используют также и несколько другую формулировку этой теоремы, подключая попутно и случай вырожденного треугольника:
Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.
Заметим, что разница между двумя приведенными формулировками столь незначительна, что нет смысла рассматривать их отдельно. В дальнейшем при решении задач мы будем использовать как первую формулировку теоремы, так и вторую, не оговаривая это отдельно.
Неравенство треугольника возникло, судя по всему, тогда же, когда человек научился ходить и хоть как-то мыслить. Известно, что одну из первых его формализаций приводит Евклид в знаменитых «Началах». Там он доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из нее выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника. Вот такая вот непростая логическая цепочка для доказательства вполне очевидного, казалось бы, неравенства!
| 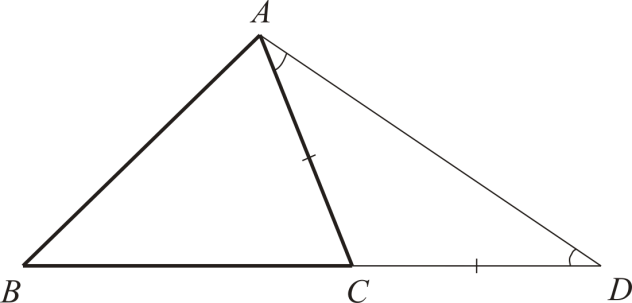 |
| Рис. 1 |
Доказательство теоремы. Рассмотрим треугольник ABC и покажем, что AB AC + BC. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления).
В треугольнике ABC (рис. 1) на продолжении стороны BC отложим отрезок CD, равный AC. В равнобедренном треугольнике ACD 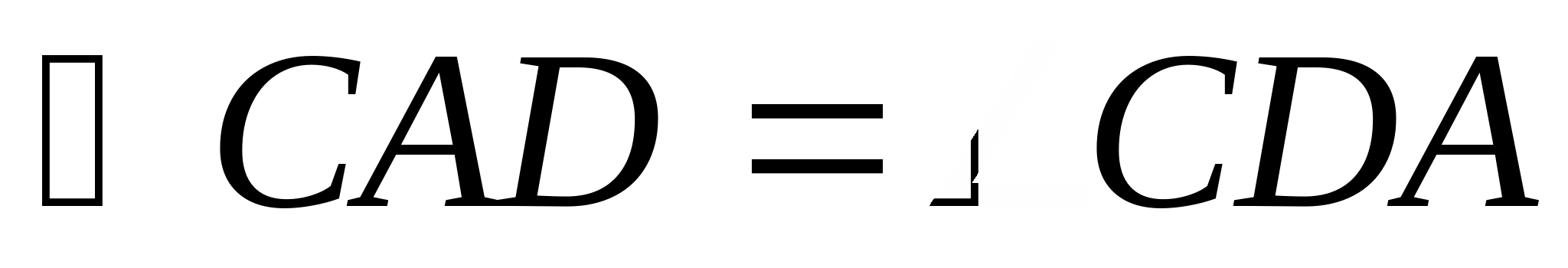 . В треугольнике ABD угол ADB меньше угла BAD, значит, BD AB, или BC + CD AB. Но CD = AC, значит, AC + BC AB.
. В треугольнике ABD угол ADB меньше угла BAD, значит, BD AB, или BC + CD AB. Но CD = AC, значит, AC + BC AB.
Замечание. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства:
AB AC + BC;
AC AB + BC;
BC AB + AC.
Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам.
Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими.
Докажите, что в треугольнике каждая сторона больше разности двух других сторон.
Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач.
В треугольнике длины двух сторон равны 5, 27 и 2, 79. Какой может быть длина третьей стороны, если известно, что она является целым числом.
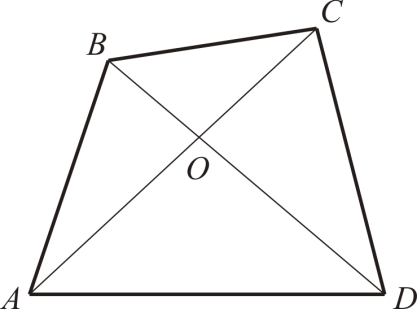
Докажите, что в произвольном четырехугольнике ABCD AB + CD AC + BD.
Докажите, что в треугольнике ABC выполнено неравенство
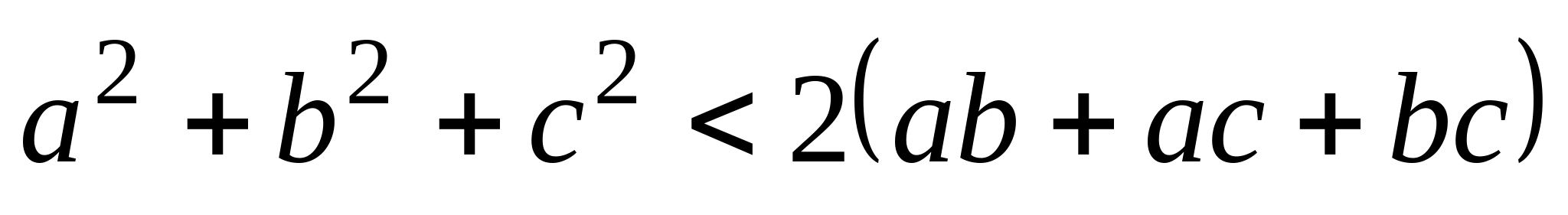 (a, b, c – стороны треугольника ABC).
(a, b, c – стороны треугольника ABC).
Докажите, что медиана AM в произвольном треугольнике ABC по длине меньше, чем 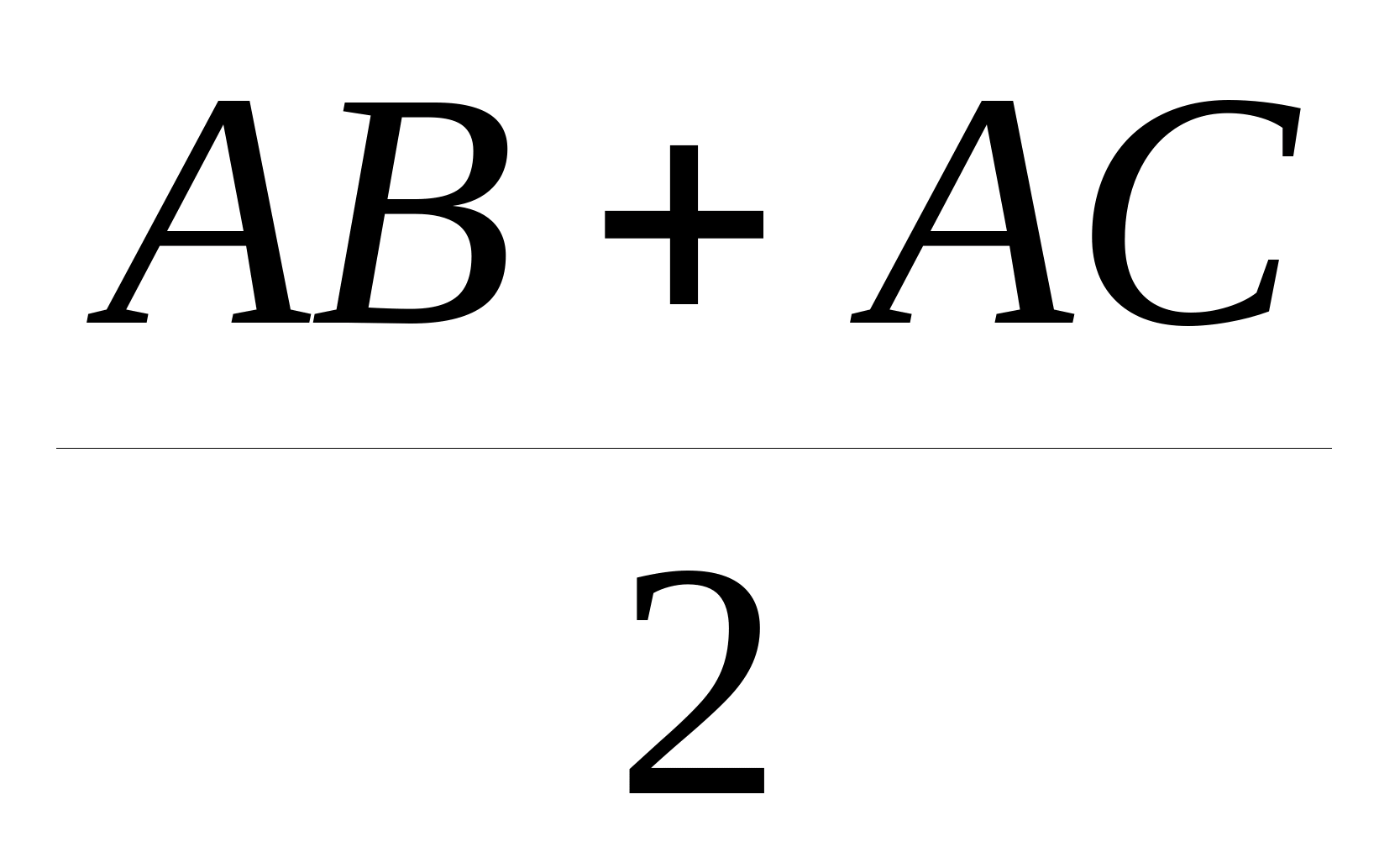 .
.
На плоскости дан квадрат ABCD и точка O. Докажите, что расстояние от точки O до одной из вершин квадрата не превосходит суммы расстояний от O до трех других вершин квадрата.
a, b и c - длины сторон произвольного треугольника. Докажите, что a = y + z, b = x + z и c = x + y, где x, y и z — положительные числа.
Пусть a, b, c – стороны треугольника. Докажите неравенство a3 + b3 + 3abc c3.
a, b и c - длины сторон произвольного треугольника. Докажите, что a2 + b2 + c2 ab + bc + ca).
a, b и c - длины сторон произвольного треугольника. Докажите, что
a(b - c)2 + b(c - a)2 + c(a - b)2 + 4abc a3 + b3 + c3.
a, b и c - длины сторон произвольного треугольника. Докажите, что
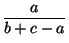 +
+ 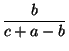 +
+ 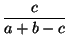
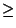 3.
3.
a, b, c – стороны треугольника. Докажите неравенство 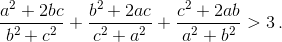
a, b, c – длины сторон треугольника. Докажите, что
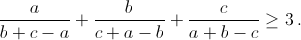 .
.
a, b и c - длины сторон произвольного треугольника. Докажите, что
(a + b - c)(a - b + c)(- a + b + c)  abc.
abc.
a, b и c - длины сторон произвольного треугольника. Докажите, что
a2b(a - b) + b2c(b - c) + c2a(c - a) 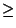 0.
0.
Длины двух сторон треугольника a и b удовлетворяют условию a b, а длины соответствующих им высот равны ha и hb.
Доказать неравенство a + ha ≥ b + hb и определить, когда достигается равенство.
Докажите, что сумма длин любых двух медиан произвольного треугольника
а) не больше ¾ P, где P – периметр этого треугольника;
б) не меньше ¾ p, где p – полупериметр этого треугольника.
Отрезки AB и CD длины 1 пересекаются в точке O , причем  AOC=60o . Докажите, что AC+BD
AOC=60o . Докажите, что AC+BD 1 .
1 .
Решение
Построим отрезок CB1 так, что четырехугольник ABB1C – параллелограмм, тогда AC=BB1 . Из треугольника BB1D получаем, что BB1+BD B1D и, следовательно, AC+BD
B1D и, следовательно, AC+BD B1D . Остается заметить, что треугольник CB1D равносторонний ( CD=CB1=1 , а
B1D . Остается заметить, что треугольник CB1D равносторонний ( CD=CB1=1 , а  B1CD=
B1CD= AOC=60o ), и, значит, B1D=1 . Таким образом, получаем AC+BD
AOC=60o ), и, значит, B1D=1 . Таким образом, получаем AC+BD 1 .
1 .
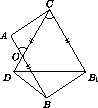
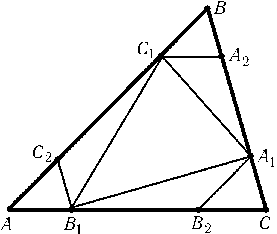
Точки C1, A1, B1 взяты на сторонах AB, BC, CA треугольника ABC так, что BA1 = 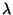 . BC, CB1 =
. BC, CB1 = 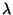 . CA, AC1 =
. CA, AC1 = 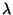 . AB, причем 1/2 P треугольника ABC и периметр P1 треугольника A1B1C1 связаны неравенствами (2
. AB, причем 1/2 P треугольника ABC и периметр P1 треугольника A1B1C1 связаны неравенствами (2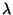 -1)P P1 P.
-1)P P1 P.
Решение
Возьмем на сторонах AB, BC, CA точки C2, A2, B2 так, что A1B2| AB, B1C2| BC, C1A2| CA (рис.). Тогда A1B1 A1B2 + B2B1 = (1 - 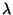 )AB + (2
)AB + (2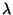 - 1)CA. Аналогично B1C1 )BC + (2
- 1)CA. Аналогично B1C1 )BC + (2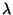 - 1)AB и C1A1 )CA + (2
- 1)AB и C1A1 )CA + (2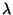 - 1)BC. Складывая эти неравенства, получаем P1 P.
- 1)BC. Складывая эти неравенства, получаем P1 P.
Ясно, что A1B1 + A1C B1C, т. е. A1B1 + (1 - 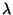 )BC
)BC 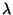 . CA. Аналогично B1C1 + (1 -
. CA. Аналогично B1C1 + (1 - 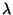 )CA
)CA 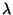 . AB и C1A1 + (1 -
. AB и C1A1 + (1 -  )AB
)AB  . BC. Складывая эти неравенства, получаем P1 (2
. BC. Складывая эти неравенства, получаем P1 (2 - 1)P.
- 1)P.
2



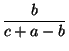 +
+ 
