Неравенства. Свойства неравенств. Задачи олимпиад.
Определение: Говорят, что действительное число a больше (меньше) действительного числа b, если их разность a-b –положительное (отрицательное) число.
Свойства:
Если ab и bc, то ac.
Если ab , то a+cb+c.
Если ab и m0, то ambm.
Если ab и mambm.
Если ab и bc, то ac.
Если ab и cd, то a+cb+d.
Если ab и cd, то acbd, a,b,c,d0.
Если ab , то anbn ,a,b  0,
0,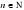 .
.
Если ab , то anbn ,n-нечетное.
Провести доказательства некоторых свойств.
Классические неравенства:
Неравенство об обратных величинах: 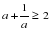
Среднее арифметическое: 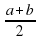
Среднее геометрическое: 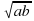
Среднее гармоническое 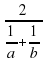
Среднее квадратичное 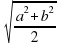
Неравенство о средних: 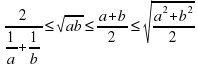
При этом неравенство между средним арифметическим и средним геометрическим 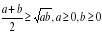 называют неравенством Коши.
называют неравенством Коши.
Неравенство Коши – Буняковского
Для любых действительных чисел 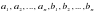 выполняется неравенство:
выполняется неравенство:
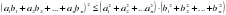
Равенство в (4) имеет место тогда и только тогда, когда числа  и
и  пропорциональны, то есть существуют такие числа
пропорциональны, то есть существуют такие числа  и
и 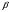 , что
, что 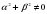 и для всех k=1,2,…,n выполняется равенство
и для всех k=1,2,…,n выполняется равенство
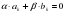 .
.
Основные методы доказательства неравенств
I. Доказательство неравенств с помощью определения
Для доказательства неравенства 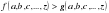 этим способом на заданном множестве значений переменных a, b, c, …, z составляют разность
этим способом на заданном множестве значений переменных a, b, c, …, z составляют разность 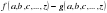 и доказывают, что она положительна при всех значениях переменных.
и доказывают, что она положительна при всех значениях переменных.
Пример 1. (Неравенство Коши)
Доказать, что при всех 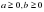 выполняется неравенство
выполняется неравенство
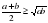 (1)
(1)
Доказательство. Составим разность 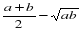 и выясним ее знак. Имеем:
и выясним ее знак. Имеем: 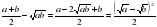 . Выражение
. Выражение 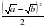 неотрицательно при любых значениях
неотрицательно при любых значениях  (условия
(условия  определяют существование
определяют существование 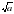 и
и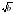 ), причем знак равенства имеет место лишь при a=b. То есть
), причем знак равенства имеет место лишь при a=b. То есть 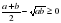 , а это означает, что
, а это означает, что 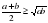 , ч.т.д.
, ч.т.д.
Пример 2. Доказать, что если 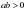 , то
, то
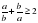 (2)
(2)
Доказательство. Имеем: 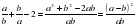 . Так как
. Так как 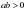 , то
, то 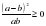 , причем знак равенства имеет место лишь при a=b. Таким образом, разность
, причем знак равенства имеет место лишь при a=b. Таким образом, разность 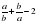 неотрицательна и неравенство (2) доказано.
неотрицательна и неравенство (2) доказано.
II. Синтетический метод доказательства неравенств
Суть этого метода заключается в том, что с помощью различных преобразований доказываемое неравенство выводят из некоторых опорных (известных) неравенств. В качестве опорных можно использовать следующие неравенства:
а) 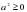 ,
,
б) неравенство Коши (1),
в) 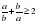 , при
, при 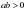 , которое является следствием (2),
, которое является следствием (2),
г) 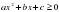 при
при 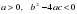 ,
,
д) 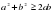 для всех чисел a и b.
для всех чисел a и b.
Пример 3. Доказать, что для любых чисел a, b и c имеет место неравенство
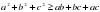 (3)
(3)
Доказательство. В качестве опорных, выберем неравенства
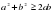 ,
, 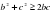 ,
, 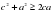
Сложим почленно эти неравенства, а затем разделим обе части полученного неравенства на два. Получим нужное нам неравенство.
Пример 4. Доказать, что для любых неотрицательных чисел a, b, c, d имеет место неравенство
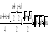
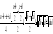 .
.
Доказательство. Воспользуемся в качестве опорных неравенствами Коши 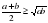 и
и 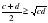 . Тогда получим:
. Тогда получим:
, ч.т.д.
III. Доказательство методом «от противного»
Метод доказательства «от противного» высказывания «из А следует В» применяют в следующей форме: считают истинным высказывание «не выполняется В» и пытаются вывести отсюда справедливость высказывания «не выполняется А». Если это удается, то получается противоречие, из которого следует, что предположение о неверности А – ошибочно. Покажем, как этот метод применяется при доказательстве неравенств.
Пример 5. Доказать, что для любого числа а выполняется неравенство
 .
.
Доказательство. Предположим противное, что для некоторого числа а рассматриваемое неравенство неверно, то есть имеет место неравенство:
 . По свойству 3 можно умножить обе части неравенства на положительное число
. По свойству 3 можно умножить обе части неравенства на положительное число  , при этом знак неравенства не изменится:
, при этом знак неравенства не изменится:  . По свойству 2 можно вычесть из обеих частей неравенства выражение
. По свойству 2 можно вычесть из обеих частей неравенства выражение  . После преобразований правой части получим:
. После преобразований правой части получим:
 , то есть
, то есть  . Последнее неравенство не выполняется ни при каком значении а, так как правая часть неравенства не может принимать отрицательные значения. Полученное противоречие доказывает верность исходного неравенства.
. Последнее неравенство не выполняется ни при каком значении а, так как правая часть неравенства не может принимать отрицательные значения. Полученное противоречие доказывает верность исходного неравенства.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Докажите, что для любых действительных чисел a и b выполняется неравенство 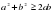 .
.
Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
Доказать, что для любых действительных чисел a и b выполняется неравенство

Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
Докажите, что если  ,
,  и
и  , то выполняется неравенство
, то выполняется неравенство

Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
Доказать, что если  , то верно неравенство
, то верно неравенство

Указание: Обозначить  и использовать в качестве опорного неравенство (3).
и использовать в качестве опорного неравенство (3).
Доказать, что для любых положительных чисел a, b и c выполняется неравенство

Указание: Воспользоваться три раза неравенством (1), где в качестве слагаемых взять, соответственно,  ,
,  в первом неравенстве,
в первом неравенстве,  ,
,  во втором неравенстве и
во втором неравенстве и  ,
,  в третьем неравенстве.
в третьем неравенстве.
Доказать, что для любых положительных чисел a, b и c выполняется неравенство

Указание: Воспользоваться в качестве опорного неравенством Коши - Буняковского.
Доказать, что если  , то верно неравенство
, то верно неравенство

Указание: доказательство провести методом от противного. Возвести обе части в квадрат и получить противоречие с неравенством Коши.
Доказать, что при  верно неравенство
верно неравенство
 .
.
Указание: доказательство провести методом от противного. Возвести обе части в квадрат и после преобразований сравнить знак левой и правой частей неравенства.
Доказать, что при  верно неравенство
верно неравенство

Указание: доказательство провести методом математической индукции.
Доказать, что при  верно неравенство
верно неравенство

Указание: доказательство провести методом математической индукции.
Дополнительные задачи:
11. Доказать неравенство
12. Доказать, что при любых значениях x и y верно неравенство
Доказательство неравенств путем преобразования очевидного или известного классического неравенства к виду доказываемого неравенства.
13. Доказать неравенство
если a, b, c — неотрицательные числа.
14. Доказать, что
если a,b,c — неотрицательные числа.
15. Доказать неравенство: ab(a+b)+bc(b+c)+ac(a+c)  6abc
6abc
16. 
17. Доказать неравенство: 
18. Докажем, что (a+b)(ab+1)  4ab, при а
4ab, при а 0, b
0, b 0.
0.
19. Доказать неравенство:
20. Докажите неравенства:
21. Докажите справедливость неравенства:
, а среднее геометрическое равно
? Ответ запишите числом.
Найдите наименьшее целое А.



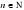 .
.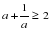
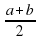
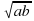
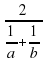
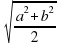
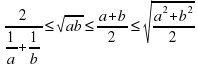
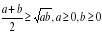 называют неравенством Коши.
называют неравенством Коши. выполняется неравенство:
выполняется неравенство: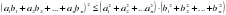
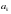 и
и 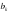 пропорциональны, то есть существуют такие числа
пропорциональны, то есть существуют такие числа  и
и 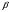 , что
, что 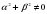 и для всех
и для всех 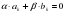 .
.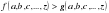 этим способом на заданном множестве значений переменных
этим способом на заданном множестве значений переменных 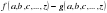 и доказывают, что она положительна при всех значениях переменных.
и доказывают, что она положительна при всех значениях переменных.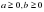 выполняется неравенство
выполняется неравенство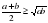 (1)
(1)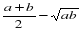 и выясним ее знак. Имеем:
и выясним ее знак. Имеем: 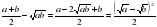 . Выражение
. Выражение 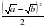 неотрицательно при любых значениях
неотрицательно при любых значениях 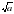 и
и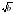 ), причем знак равенства имеет место лишь при
), причем знак равенства имеет место лишь при 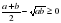 , а это означает, что
, а это означает, что 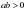 , то
, то 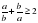 (2)
(2)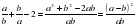 . Так как
. Так как 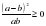 , причем знак равенства имеет место лишь при
, причем знак равенства имеет место лишь при 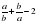 неотрицательна и неравенство (2) доказано.
неотрицательна и неравенство (2) доказано. 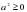 ,
, 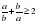 , при
, при 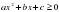 при
при 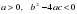 ,
, 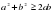 для всех чисел
для всех чисел 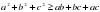 (3)
(3)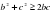 ,
, 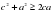
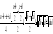 .
.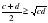 . Тогда получим:
. Тогда получим: