Методы решения олимпиадных задач: инварианты, правило крайнего, подсчет двумя способами.

ИНВАРИАНТЫ

Задача 1. Не вычисляя сумму 1 + 2 + 3 + ... + 2017; 
скажите, является она четной или нет.

Задача 2. Существуют ли целые числа a и b, такие что ab(a+b)=201500010002015?

Задача 3. На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными?

Задача 4. 100 фишек выставлены в ряд. Разрешено менять местами две фишки, стоящие через одну фишку. Можно ли с помощью таких операций переставить все фишки в обратном порядке?

Задача 5. Дана квадратная таблица 4*4, в каждой клетке которой стоит знак "+" или "-":
 

За один ход можно поменять знаки на противоположные в любой строке или любом столбце. Можно ли через несколько ходов получить таблицу из одних плюсов?

Задача 6. Вася разозлился на карикатуру в школьной газете и порвал ее на 4 части, затем взял один из получившихся кусочков и тоже порвал на 4 части, затем снова взял один из кусочков – и так до тех пор, пока вся злость не вышла. Могло ли у Васи вконце получиться 2016 клочков бумаги? А 2017?

Задача 7. 2000 чисел х₁, х₂,…, х₂₀₀₀ записаны в строчку. Известно, что сумма любых трех соседних из них равна 200. При этом первое число равно 19, последнее 98. Найдите остальные 1998 чисел.

Задача 8. На острове Серобуромалин живет 13 серых, 15 бурых и 17 малиновых хамелеонов. Когда встречаются два хамелеона разного цвета, они одновременно перекрашиваются в третий цвет. Может ли через некоторое время оказаться, что все хамелеоны имеют один цвет?

Задача 9. Круг разделен на шесть секторов. В каждом секторе написано число. Разрешается одновременно увеличивать числа в двух соседних секторах на один. Можно ли сделать все числа равными, если в начале они такие: 1,0,1,0,0,0?

Задача 10. Даны три числа: 2015, 2016 и 2017. За один ход разрешается заменить числа 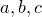 на числа 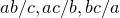. Можно ли через несколько ходов получить числа 2018, 2019 и 2020?

Подсчет двумя способами.

1. Можно ли в прямоугольной таблице 5×10 так расставить числа, чтобы сумма чисел каждой строки равнялась бы 30, а сумма чисел каждого столбца равнялась бы 10?

2. Рита, Люба и Варя решали задачи. Чтобы дело шло быстрее, они купили конфет и условились, что за каждую решённую задачу девочка, решившая её первой, получает четыре конфеты, решившая второй  — две, а решившая последней  — одну. Девочки говорят, что каждая из них решила все задачи и получила 20 конфет, причём одновременных решений не было. Они ошибаются. Как вы думаете, почему?

3. Несколько шестиклассников и семиклассников обменялись рукопожатиями. При этом оказалось, что каждый шестиклассник пожал руку семи семиклассникам, а каждый семиклассник пожал руку шести шестиклассникам. Кого было больше - шестиклассников или семиклассников?

4. 10 друзей послали друг другу праздничные открытки, так что каждый послал 5 открыток. Докажите, что найдутся двое, которые послали открытки друг другу.

5. Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и чёрных пятиугольников. Каждый чёрный лоскут граничит только с белыми, а каждый белый — с тремя чёрными и тремя белыми. Сколько лоскутков белого цвета?

6. Каждый участник двухдневной олимпиады в первый день решил столько же задач, сколько все остальные в сумме – во второй день. 
   Докажите, что все участники решили поровну задач.

7. В банановой республике прошли выборы в парламент, в котором участвовали все жители. Все голосовавшие за партию "Мандарин" любят мандарины. Среди голосовавших за другие партии 90% не любят мандарины. Сколько процентов голосов набрала партия "Мандарин" на выборах, если ровно 46% жителей любят мандарины?

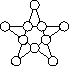
8. Можно ли в кружочки на пятиконечной звезде (см. рисунок) расставить 4 единицы, 3 двойки и 3 тройки так, чтобы суммы четырех чисел, стоящих на каждой из пяти прямых, были равны? 
   
   
   

9. Четыре друга пришли с рыбалки. Каждые двое сосчитали суммы своих уловов. Получилось шесть чисел: 7, 9, 14, 14, 19, 21. Сможете ли Вы узнать, каковы были уловы?

10. В конкурсе пения участвовали Петух, Ворона и Кукушка. Каждый член жюри проголосовал за одного из трех исполнителей. Дятел подсчитал, что в жюри было 59 судей, причем за Петуха и Ворону было в сумме подано 15 голосов, за Ворону и Кукушку – 18 голосов, за Кукушку и Петуха – 20 голосов. Дятел считает плохо, но каждое из четырёх названных им чисел отличается от правильного не более чем на 13. Сколько судей проголосовали за Ворону?

11. Можно ли в клетки квадрата 10×10 поставить некоторое количество звёздочек так, чтобы в каждом квадрате 2×2 было ровно две звёздочки, а в каждом прямоугольнике 3×1 – ровно одна звёздочка? (В каждой клетке может стоять не более одной звёздочки.)

12. На столе в виде треугольника выложены 28 монет одинакового размера (рис.). Известно, что суммарная масса любой тройки монет, которые попарно касаются друг друга, равна 10  г. Найдите суммарную массу всех 18  монет на границе треугольника. 

Принцип крайнего.

1. На бесконечном листе клетчатой бумаги в каждой клетке записано некоторое натуральное число. Известно, что число в каждой клетке равно среднему арифметическому четырех чисел, записанных в клетках, смежных с данной. Доказать, что все записанные числа равны друг другу.

2. Семь грибников собрали вместе 100 грибов, причем никакие двое не собрали одинакового числа грибов. Докажите, что есть трое грибников, собравших вместе не менее 50 грибов.

3. Давным-давно страной Тарнией правил царь Ятианр. Чтобы тарнийцы поменьше рассуждали, он придумал для них простой язык. Его алфавит состоял всего из шести букв: А, И, Н, Р, Т, Я, но порядок их отличался от принятого в русском языке. Словами этого языка были все последовательности, использующие каждую из этих букв по одному разу. Ятианр издал полный словарь нового языка. В соответствии с алфавитом первым словом словаря оказалось "Тарния". Какое слово следовало в словаре за именем Ятианр?