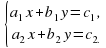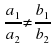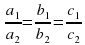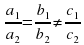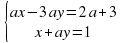Уравнения с параметрами.

Файл к уроку

Решение уравнений с параметрами.

Не так давно 8 класс познакомился с квадратными уравнениями и алгоритмами их решения. Сегодня мы рассмотрим еще один вид уравнений, который часто встречается на олимпиадах и турнирах, и включен в ЕГЭ по профильной математике – это уравнения с параметром. Что такое параметр? Обычно это число, в зависимости от значения которого уравнение, будь оно линейным или квадратным, может иметь корни, а может их не иметь.

Задачи с параметрами считаются сложными ,однако если разобраться досконально, из каких шагов состоит путь к решению уравнения, то параметр уже не кажется такой злобной величиной.

Линейные уравнения с параметрами.

Уравнение вида

где a, b из R, x - переменная, называется уравнением первой степени (линейным уравнением).

Уравнение равносильно уравнению

ax = – b

откуда следует следующее утверждение.

1. Если a ≠ 0, то уравнение имеет единственное решение x = – ^b/_a;

2. Если a = 0, b ≠ 0, то множество решений уравнения пусто;

3. Если a = 0, b = 0, то любое действительное число является решением уравнения.

Решить уравнение с параметром – значит указать решение при всех значениях параметра, то есть фактически решить бесконечное множество уравнений, объединив их в одно по неким схожим зависимостям от параметра.

Пример 1. Решить уравнение: a²x – 1 = x + a.

Пример 2. Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = -а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)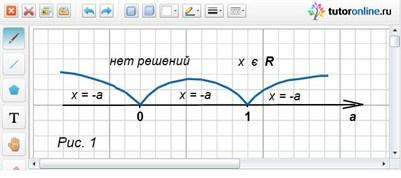

Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.

Пример 4. При каких значениях параметра b уравнение не имеет корней: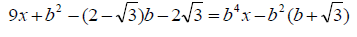

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 5. Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение. Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).

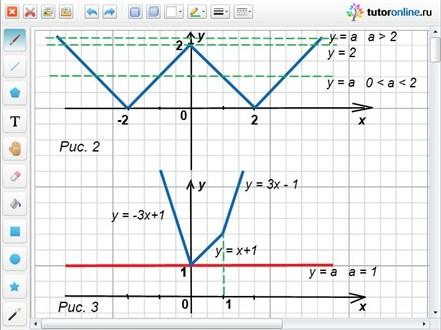
На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а a 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 a

Пример 6. При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций  y = 2|x| + |x – 1| и y = a. Для  y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

      {-3x + 1, при x

y = {x + 1, при  0 ≤ x ≤ 1,

      {3x – 1, при x 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 7. При каких значениях параметра а неравенство имеет решением все действительные числа:

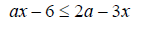
Системы линейных уравнений с параметрами.

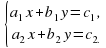
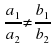– Система имеет единственное решение.

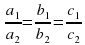– Система имеет бесконечное множество решений.

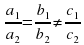– Система не имеет решений.

Пример 8. Для всех значений параметра а решить систему уравнений

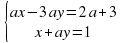
Квадратичные уравнения с параметрами.

Решение уравнений второй степени сводится к исследованию поведения квадратного трехчлена, исследованию знака дискриминанта при различных значениях параметра. Часто при решении нам может помочь теорема Виета, когда вопрос стоит о корнях разных знаков, о корнях одного знака.

Квадратное уравнение 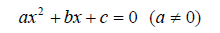может не иметь решений (Da=0 или D=0), два решения (D0) или бесконечное множество решений (когда при каком-то значении параметра получаем 0=0).

Пример 9. Решить уравнение в зависимости от параметра а:

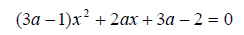
Пример 10. При каких значениях 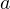корни уравнения 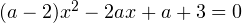положительны?

Пример 11. Найти значения параметра а, при которых среди корней уравнения имеется ровно один отрицательный: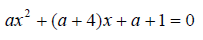

Пример 12. Найти все значения параметра а, при которых уравнение имеет два различных отрицательных корня:

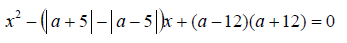
Пример 13. При каких значениях m корни уравнения 4x² – (3m + 1) x – m – 2 = 0 лежат в промежутке между –1 и 2?

Пример 14: Найти все значения параметра а, при которых меньший корень уравнения x² + (a + 1) x + 3 = 0 лежал в интервале (–1; 3)