Конспект занятия "Задача 16 (С 4). Планиметрия."
Вневписанная окружность
Определение вневписанной окружности.
Рассмотрим треугольник АВС. Продолжим его стороны за точки В и С. Проведём биссектрисы внешних углов В и С. Они пересекутся в точке Ка. Эта точка равноудалена от лучей АВ и ВС и от лучей АС и СВ. Значит, Ка равноудалена от всех трех прямых АВ, ВС и СА, поэтому существует окружность с центром в точке Ка, касающаяся стороны ВС и продолжений сторон АВ и АС. Расстояния от Ка до ВС, ВК1 и СК2 - это радиусы построенной окружности. Заметим, что через Ка проходит и биссектриса угла А треугольника АВС
Аналогично можно построить окружности, касающиеся двух других сторон. Всего у треугольника имеется три вневписанных окружности.
Итак, определение:
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
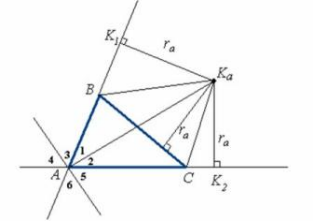
Свойства вневписанной окружности.
Выясним, как связаны радиусы вневписанных окружностей с другими элементами треугольника.
Свойство 1.Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника (1)

Свойство 2.Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника
АВ1 = АС1 = p

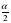 Теорема1. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. ra = p·tg
Теорема1. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. ra = p·tg 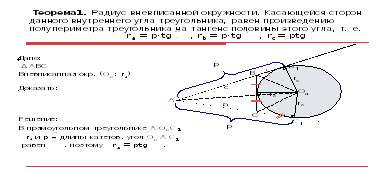
Теорема 2. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е.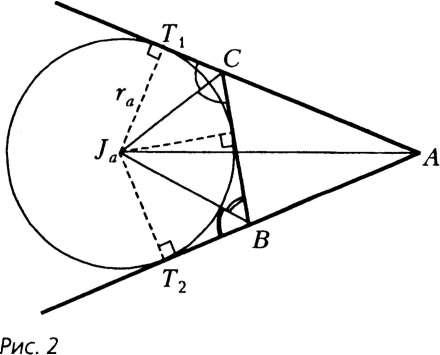
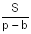
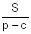
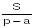
ra = , rb = , rc =
Доказательство. Легко видеть, что
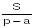
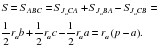
Т.е. ra =
Теорема3. Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности, т. е.
ra + rb + rc = r + 4R .
Теорема 4. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е.
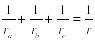
Теорема 5. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е.
rarb + rbrc + rcra = p2
Теорема 6. Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника, т.е.
rarbrc = rp2
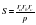 Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.
Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.
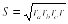 Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е.
Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е.
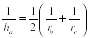
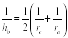
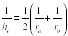 Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.
Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.
, , .
.
.





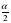 Теорема1. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е.
Теорема1. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. 

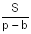
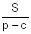
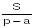
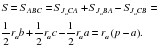
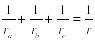
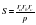 Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.
Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е. 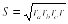 Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е.
Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е. 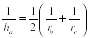
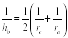
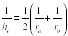 Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.
Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.