Файл к занятию 14
Самостоятельная работа
| Задание 1. Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 20. Найдите площадь боковой поверхности этой пирамиды. Ответ: 1152 |
|

Задание 2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Ответ: 8.
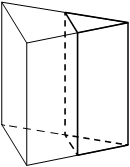
Задание 3. В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ: 342

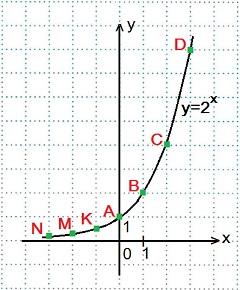
Показательная функция, ее свойства и график
Функцию вида y=ax, где а0, a≠1, х – любое число, называют показательной функцией.
1)Область определения показательной функции: D (y)=R – множество всех действительных чисел.
2)Область значений показательной функции: E(y)=R+ - множество всех положительных чисел.
3)Показательная функция y = ax является возрастающей на множестве всех действительных чисел, если a 1, и убывающей, если 0 .
Свойства степени с рациональным показателем
Пусть дано положительное число a и произвольное рациональное число n. Число 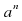 называется степенью, число a — основанием степени, число n — показателем степени. По определению полагают:
называется степенью, число a — основанием степени, число n — показателем степени. По определению полагают:
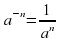 ;
; 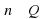
Если 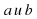 и — положительные числа,
и — положительные числа, 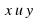 — любые рациональные числа, то справедливы следующие свойства:
— любые рациональные числа, то справедливы следующие свойства:
Решение показательных уравнений вида af(x) =a g(x)
Следствие из теоремы о свойствах показательной функции. Пусть 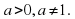 Если степени с основанием
Если степени с основанием 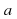 равны, то их показатели равны, т.е. если af(x) =a g(x), то f(x)=g(x)
равны, то их показатели равны, т.е. если af(x) =a g(x), то f(x)=g(x)
Найдите корень уравнения:
8x + 5 = 64. Ответ:-3
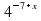 = 64.Ответ: 10
= 64.Ответ: 10
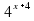 = 64. Ответ:-1
= 64. Ответ:-1
Задание 1. Найдите корень уравнения 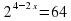 . Ответ: −1.
. Ответ: −1.
Задание 2. Найдите корень уравнения 62 − 4x = 363x. Ответ: 0,2.
Задание 3. Найдите корень уравнения 16х-9= 0,5. Ответ: 8,75.
Задание 4. Найдите корень уравнения: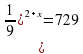 . Ответ: −5.
. Ответ: −5.
Задание 5. Найдите корень уравнения: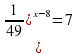 . Ответ: 7,5.
. Ответ: 7,5.
Дополнительно:
Задание 1. Найдите корень уравнения (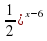 =
=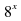 . Ответ:1,5
. Ответ:1,5
Задание 2. Найдите корень уравнения: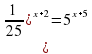 .Ответ: −3.
.Ответ: −3.
Задание 3. Решите уравнение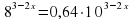 .Ответ: 0,5.
.Ответ: 0,5.
Решение показательных уравнений способом вынесения общего множителя за скобки
Задание 6. Решите уравнение 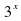 - 2
- 2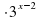 =63. Ответ: 4
=63. Ответ: 4
Задание 7. Решите уравнение 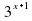 - 2
- 2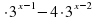 =17. Ответ: 2
=17. Ответ: 2
Решение показательных уравнений способом введения замены
Задание 8. Решите уравнение 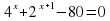 . Ответ: 3
. Ответ: 3
Задание 9. Решите уравнение 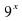 -
- 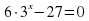 . Ответ: 2
. Ответ: 2
Задание 10. Решите уравнение 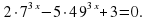 Ответ: 0
Ответ: 0
Логарифм. Свойства логарифмов
Решите уравнение 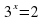
Множеством (областью значений) показательной функии у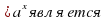 множество всех положительных чисел. Значит, для любого положительного числа в найдется такое значение аргумента с, что
множество всех положительных чисел. Значит, для любого положительного числа в найдется такое значение аргумента с, что
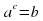
Такое значение аргумента единственное. Это единственное значение аргумента называют логарифмом числа в по основанию а и обозначают с = logab.
Пусть а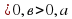 ≠1. Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число в.
≠1. Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число в.
Вычислить: 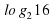 ;
; 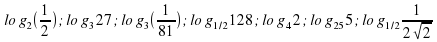
Задание 11. Найдите значение выражения 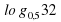 .Ответ: −5.
.Ответ: −5.
Задание 12. Найдите значение выражения 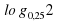 .Ответ: −0,5.
.Ответ: −0,5.
Основное логарифмическое тождество 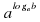 =b
=b
Вычислить: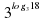 =18;
=18;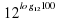 =100;
=100; 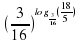 =18/5;
=18/5;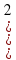
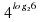 =36
=36
Задание 13. Найдите значение выражения  .Ответ: 169.
.Ответ: 169.
Задание 14. Найдите значение выражения  . Ответ:
. Ответ: 
Задание 15. Найдите значение выражения  . Ответ: 25.
. Ответ: 25.
Виды логарифмов
loga b - логарифм числа b по основанию a (a 0, a ≠ 1, b 0)
lg b - десятичный логарифм (логарифм по основанию 10, a = 10).
ln b - натуральный логарифм (логарифм по основанию e, a = e).
Свойства логарифмов
При любых  верно равенство:
верно равенство:
logaa = 1
loga1 = 0
loga(bc) = logab + logac
loga( ) = logab - logac
) = logab - logac
loga bp = p logab
loga  = -logab
= -logab
logak b =  loga b, при k ≠ 0
loga b, при k ≠ 0
logb c =  - формула перехода к новому основанию
- формула перехода к новому основанию

Задание 16. Найдите значение выражения log560-log512. Ответ: 1.
Задание 17. Найдите значение выражения log3 8,1+ log3 10. Oтвет: 4.
Задание 18. Найдите значение выражения log 0,55 20 – log 0,55 11 .Oтвет: −1.
Дополнительное задание:
1. Найдите значение выражения log411−log42,75. Ответ:1
2.Найдите значение выражения log3121,5−log31,5. Ответ: 4
Задание 19. Найдите значение выражения log95/log815. Ответ:2
Задание 20. Найдите значение выражения log53⋅log3125. Ответ: 3
Задание 21. Найдите значение выражения log35⋅log527. Ответ:3
Логарифмическая функция Функция вида y = loga х (где а 0, а ≠ 1) называется логарифмической. 1) Область определения логарифмической функции — множество всех положительных чисел. Это следует из определения логарифма, так как выражение logax имеет смысл только при x 0. 2) Множество значений логарифмической функции — множество R всех действительных чисел.
3) Логарифмическая функция y = logax является возрастающей на промежутке x 0, если a 1, и убывающей, если 0 .
4) Если a 1, то функция y = logax принимает положительные значения при x 1, отрицательные — при 0 . Если 0 , то функция y = logax принимает положительные значения при 0 , отрицательные — при x 1.
Рассмотрим решение уравнений, в которых переменная находится под знаком логарифма. Известно, что для любого действительного числа b есть такое положительное число x, что logax = b, т.е. уравнение logax = b имеет корень. Такой корень существует и равен x = ab, так как logaab = b.
Пусть  . Если
. Если 
 , то
, то  =
=

 ⇔
⇔
Решение логарифмических уравнений на основании определения логарифма
Задание 22. Найдите корень уравнения log3(3+6x)=2. Ответ: 1
Задание 23. Найдите корень уравнения log4(12+4x)=3. Ответ: 13
Задание 24. Найдите корень уравнения log1/4(12-4х)=-3 .Ответ: −13.
Решение логарифмических уравнений на основании свойств логарифма
Задание 25. Найдите корень уравнения log6(8-х)= log63 . Ответ: 5.
Задание 26. Найдите корень уравнения log5(5-х)= 2log53 .Ответ: −4.
Задание 27. Найдите корень уравнения log7(x+9)=log7(2x-11) .Ответ: 20.
.
.






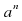 называется степенью, число
называется степенью, число 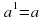
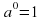
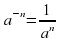
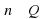
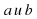 и — положительные числа,
и — положительные числа, 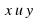 — любые рациональные числа, то справедливы следующие свойства:
— любые рациональные числа, то справедливы следующие свойства: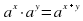
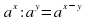
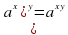
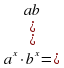
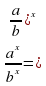
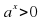
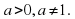 Если степени с основанием
Если степени с основанием 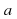 равны, то их показатели равны, т.е. если
равны, то их показатели равны, т.е. если 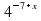
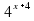 = 64. Ответ:-1
= 64. Ответ:-1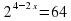 . Ответ: −1.
. Ответ: −1.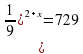 . Ответ: −5.
. Ответ: −5.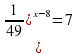 . Ответ: 7,5.
. Ответ: 7,5.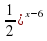 =
=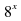 . Ответ:1,5
. Ответ:1,5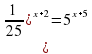 .Ответ: −3.
.Ответ: −3.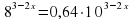 .Ответ: 0,5.
.Ответ: 0,5.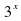 - 2
- 2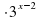 =63. Ответ: 4
=63. Ответ: 4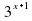 - 2
- 2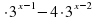 =17. Ответ: 2
=17. Ответ: 2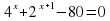 . Ответ: 3
. Ответ: 3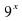 -
- 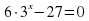 . Ответ: 2
. Ответ: 2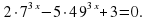 Ответ: 0
Ответ: 0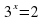
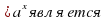 множество всех положительных чисел. Значит, для любого положительного числа в найдется такое значение аргумента с, что
множество всех положительных чисел. Значит, для любого положительного числа в найдется такое значение аргумента с, что 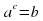
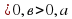 ≠1. Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число в.
≠1. Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число в. 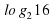
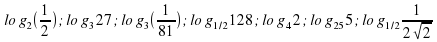
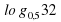 .Ответ: −5.
.Ответ: −5.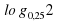 .Ответ: −0,5.
.Ответ: −0,5.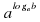 =
=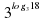
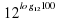 =100;
=100; 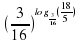
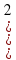
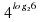 =36
=36