Конспект занятия "Задача 19 (С6). Последовательности и прогрессии."
Арифметическая и геометрическая прогрессии.
Прогрессия - последовательность чисел, получаемых по некоторому правилу. Числа составляющие последовательность, называются ее членами.
Прогрессии:
Арифметическая прогрессия
Арифметическая прогрессия - это последовательность чисел, в которой каждый член получается из предыдущего путем прибавления к нему одного и того же числа d, называемого разностью этой арифметической прогрессии.
Формула n-го члена:
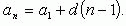
Формулы суммы n первых членов:
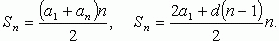
Свойства арифметической прогрессии:
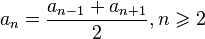
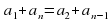
Геометрическая прогрессия
Геометрическая прогрессия - это последовательность чисел, каждое из которых равно предыдущему, умноженному на некоторое постоянное для данной прогрессии число q, называемое знаменателем этой геометрической прогрессии.
Формула n-го члена: 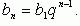
Формулы суммы n первых членов: 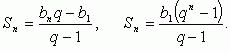
Сумма бесконечной прогрессии: 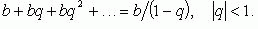
Свойства геометрической прогрессии:
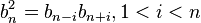
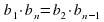
Задачи:
В арифметической прогрессии 10 членов. Сумма членов с четными номерами равна А, сумма членов с нечетными номерами равна В. Чему равна разность этой прогрессии?
Несколько последовательных натуральных чисел сложили и получили 2014. Какое максимальное количество могло быть?
Даны n различных натуральных чисел, составляющих арифметическую прогрессию 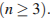
а) Может ли сумма всех данных чисел быть равной 10?
б) Каково наибольшее значение n, если сумма всех данных чисел меньше 1000?
в) Найдите все возможные значения n, если сумма всех данных чисел равна 129.
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1008 и
а) пять;
б) четыре;
в) три
из них образуют геометрическую прогрессию?
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076.
а) может ли в последовательности быть три члена?
б) может ли в последовательности быть четыре члена?
в) может ли в последовательности быть меньше 2076 членов?
Целые числа x, y, z в указанном порядке образуют геометрическую прогрессию.
а) Могул ли числа x+3, y2 и z+5 образовывать в указанном порядке арифметическую прогрессию?
б) Могут ли числа 5x, y и 3z образовывать в указанном порядке арифметическую прогрессию?
в) Найдите все x, y и z, при которых числа 5x+3, y2 и 3z+5 будут образовывать в указанном порядке арифметическую прогрессию?
Бесконечная арифметическая прогрессия, состоящая из различных натуральных чисел, первый член которой меньше 10, не содержит ни одного числа вида 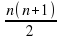 . Какое наименьшее значение может принимать сумма первых 10 членов этой прогрессии?
. Какое наименьшее значение может принимать сумма первых 10 членов этой прогрессии?
Каждое из чисел a1, a2, …, a350 равно 1, 2, 3 или 4. Обозначим
S1 = a1+a2+...+a350,
S2 = a12+a22+...+a3502,
S3 = a13+a23+...+a3503,
S4 = a14+a24+...+a3504.
Известно, что S1 = 513.
а) Найдите S4, если еще известно, что S2 = 1097, S3 = 3243.
б) Может ли S4 = 4547 ?
в) Пусть S4 = 4745. Найдите все значения, которые может принимать S2.
, если |x|<1.


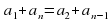
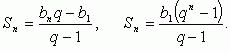
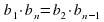
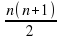 .
.