Задача 19. Теория чисел. Делимость.
Как правило, большинство учащихся, сдающих ЕГЭ по математике, к последней задаче не готовятся, ибо бытует мнение, что она слишком сложная и сделать ее нереально. На самом деле задача, за которую дают 4 первичных балла, не так страшна.
Задача на делимость содержит 3 пункта, решение первого не сложнее простейших задач из тестовой части, и чаще всего требует либо приведение примера, подобрать который не составит труда, либо простых рассуждений. Решение пункта б потребует знаний простейших формул или свойств чисел и тоже не так страшно, хотя за решение и пункта а, и пункта б дают по одному первичному баллу, терять которые из-за домыслов «я не справлюсь» нет смысла. За третий пункт в задаче дается 2 первичных балла, он уже потребует знаний более глубоких, но как мы увидим сегодня иногда задача 19 не сложнее текстовой, просто требует минимального умения рассуждать и знаний по теории чисел.
На сегодняшнем занятии обязательными знаниями будут знания признаков делимости, определений и свойств НОД и НОК, представление о четности суммы\разности четных и нечетных чисел. Все это мы рассмотрим на конкретных задачах.
Имеется 8 карточек. На них записывают по одному каждое из чисел:
−11, 12, 13, −14, −15, 17, −18, 19.
Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному из чисел:
−11, 12, 13, −14, −15, 17, −18, 19.
После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 117?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Петя умножил некоторое натуральное число на соседнее натуральное число, и получил произведение, равное а. Вася умножил некоторое четное натуральное число на соседнее четное натуральное число и получил произведение, равное b.
а) Может ли модуль разности чисел a и b равняться 8?
б) Может ли модуль разности чисел a и b равняться 11?
в) Какие значения может принимать модуль разности чисел a и b?
Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке не убывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8, 10.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 90?
б) Может ли частное этого числа и суммы его цифр быть равным 88?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
а) Можно ли число 2016 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.
Известно, что a, b, c и d – попарно различные положительные двузначные числа.
а) Может ли выполняться равенство 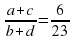 ?
?
б) Может ли дробь 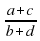 быть в 11 раз меньше, чем сумма
быть в 11 раз меньше, чем сумма 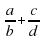 ?
?
в) Какое наименьшее значение может принимать дробь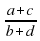 , если
, если 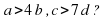
Множество чисел назовём хорошим, если его можно разбить на два подмножества с одинаковой суммой чисел.
а) Является ли множество {100; 101; 102; ...; 199} хорошим?
б) Является ли множество {2; 4; 8; ...; 2200} хорошим?
в) Сколько хороших четырёхэлементных подмножеств у множества {3; 4; 5; 6; 8; 10; 12}?
Длины сторон прямоугольника ― натуральные числа, а его периметр равен 4000. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n ― также натуральное число.
а) Какое наибольшее значение может принимать площадь прямоугольника?
б) Какое наименьшее значение может принимать площадь прямоугольника?
в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n.
У каждого ученика в классе дома живёт кошка или собака, а у некоторых, возможно, — и кошка, и собака. Известно, что мальчиков, имеющих собак, не более 1/4 от общего числа учеников, имеющих собак, а мальчиков, имеющих кошек не более 5/11 от общего числа учеников, имеющих кошек.
а) Может ли быть в классе 11 мальчиков, если дополнительно известно, что всего в классе 21 ученик?
б) Какое наибольшее количество мальчиков может быть в классе, если дополнительно известно, что всего в классе 21 ученик?


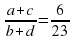 ?
?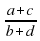 быть в 11 раз меньше, чем сумма
быть в 11 раз меньше, чем сумма 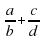 ?
?