Занятие 4. Задачи на оптимальный выбор.
В задаче 17 встречаются не только задания на проценты, кредиты и вклады, но и задачи на оптимальный выбор, это задачи, требующие знаний не столько в составлении уравнений, сколько в составлении и умении оценить граничные значения функции. Для этого нам нужно знать способы нахождения наименьшего и наибольшего значения функции.
Для нахождения наибольшего и наименьшего значений можно найти производную составленной функции, вычислить ее нули и посмотреть, как изменяются знаки при прохождении через эти точки. Если задача найти наибольшее значение – ищем точку максимума и вычисляем значение функции в этой точке. Для нахождения наименьшего значения используем точку минимума.
Полезно знать при решении таких задач и способы, позволяющие обойтись без производной. Если составленная функция квадратичная – ее максимум и минимум зависят от направления ветвей и координат вершины параболы 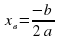 . Если ветви вверх, вершина параболы – точка минимума, если вниз – наоборот.
. Если ветви вверх, вершина параболы – точка минимума, если вниз – наоборот.
Если составленная функция линейная, то речь пойдет о наибольшем и наименьшем значении функции на отрезке, а их она принимает только на концах исследуемого отрезка.
Также не лишним будет вспомнить некоторые классические неравенства, помогающие при решении задач, например, неравенство о взаимно обратных числах и неравенство о средних.
При положительном a 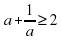 , причем равенство достигается только при
, причем равенство достигается только при 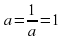 . Если же а отрицательно, то
. Если же а отрицательно, то 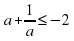 , где равенство возможно лишь при
, где равенство возможно лишь при 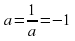 .
.
При неотрицательных a и b среднее арифметическое не меньше среднего геометрического (неравенство Коши): 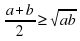 . Равенство достигается, если a=b.
. Равенство достигается, если a=b.
Как и на предыдущих занятиях, стараемся пользоваться таблицей при составлении математической модели задачи.
Задачи к уроку.
Задание 1. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей? В ответ запишите полученную сумму процентов, округлив ее до целых чисел.
Задание 2. Алексей вышел из дома на прогулку со скоростью v км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение v, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
Задание 3. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Задание 4. В бассейн проведены три трубы. Первая труба наливает 30 м3 воды в час. Вторая труба наливает в час на 3V м3меньше, чем первая (0 V V м3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?
Задание 5. Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t3 часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t3часов в неделю, они производят t приборов.
За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?
Задание 6. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Задание 7. На каждом из двух заводов работает по 100 человек. На первом заводе один рабочий изготавливает за смену 3 детали А или 1 деталь В. На втором заводе для изготовления t деталей (и А, и В) требуется t2 человеко-смен. Оба завода поставляют детали на комбинат, где собирают изделие, причем для его изготовления нужна 1 деталь А и 3 детали В. При этом заводы договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
Задание 8. Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они произведут t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Задание 9. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t 2 часов в неделю, то за эту неделю они производят 2t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t 2 часов в неделю, то за эту неделю они производят 5t единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?
Задание 10. Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
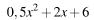 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит 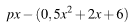 . Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
. Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?

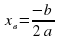 . Если ветви вверх, вершина параболы – точка минимума, если вниз – наоборот.
. Если ветви вверх, вершина параболы – точка минимума, если вниз – наоборот.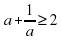 , причем равенство достигается только при
, причем равенство достигается только при 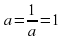 . Если же а отрицательно, то
. Если же а отрицательно, то 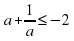 , где равенство возможно лишь при
, где равенство возможно лишь при 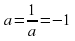 .
.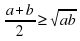 . Равенство достигается, если
. Равенство достигается, если