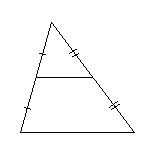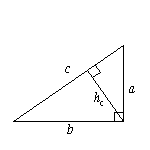Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами.
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.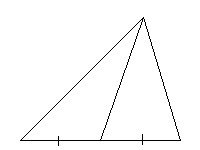
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Биссектриса
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.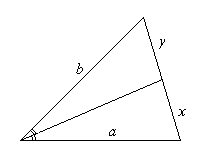
Свойства биссектрис треугольника
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам: 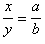 .
.
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.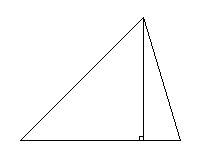
Свойства высот треугольника
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Серединный перпендикуляр
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника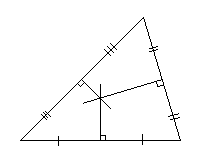
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.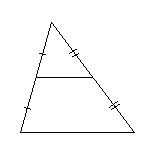
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
![]()
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности: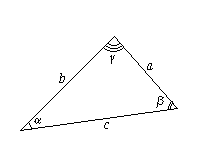
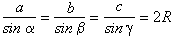
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2= b2+ c2- 2bc cos 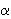
Формулы площади треугольника
Произвольный треугольник
a, b, c — стороны; 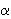 — угол между сторонами a и b;
— угол между сторонами a и b;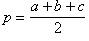 — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; ha — высота, проведенная к стороне a.
— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; ha — высота, проведенная к стороне a.
S = 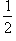 aha
aha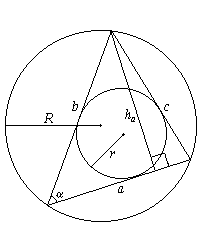
S = 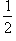 ab sin
ab sin 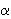
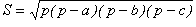
S = pr
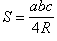
Прямоугольный треугольник
a, b — катеты; c — гипотенуза; hc — высота, проведенная к стороне c.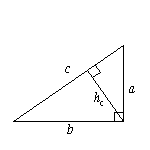
S = 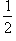 ab
ab
S = 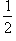 chc
chc
Равносторонний треугольник
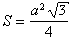

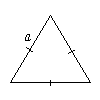
Четырехугольники
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.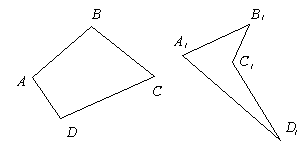
Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники бывают выпуклые (как ABCD) и невыпуклые (A1B1C1D1).
![]()
Виды четырёхугольников
Параллелограмм
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма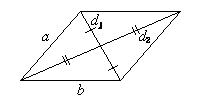
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180°;
сумма квадратов диагоналей равна сумме квадратов всех сторон:
d12+d22=2(a2+b2).
Признаки параллелограмма
Четырехугольник является параллелограммом, если:
Две его противоположные стороны равны и параллельны.
Противоположные стороны попарно равны.
Противоположные углы попарно равны.
Диагонали точкой пересечения делятся пополам.
Трапеция
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны.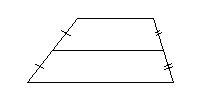
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
ее средняя линия параллельна основаниям и равна их полусумме;
если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
если трапеция равнобокая, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Признаки трапеции
Четырехугольник является трапецией, если его параллельные стороны не равны
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника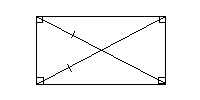
Признаки прямоугольника
Параллелограмм является прямоугольником, если:
Один из его углов прямой.
Его диагонали равны.
Ромб
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства ромба
Все свойства параллелограмма;
диагонали перпендикулярны;
диагонали являются биссектрисами его углов.
Признаки ромба
Параллелограмм является ромбом, если:
Две его смежные стороны равны.
Его диагонали перпендикулярны.
Одна из диагоналей является биссектрисой его угла.
Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства квадрата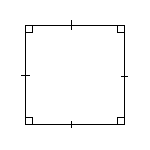
все углы квадрата прямые;
диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Признаки квадрата
Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
![]()
Основные формулы
Произвольный выпуклый четырехугольник
d1, d2 — диагонали; 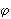 — угол между ними; S — площадь.
— угол между ними; S — площадь.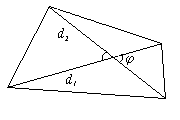
S =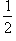 d1d2 sin
d1d2 sin 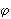
Параллелограмм
a и b — смежные стороны; 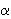 — угол между ними; ha — высота, проведенная к стороне a.
— угол между ними; ha — высота, проведенная к стороне a.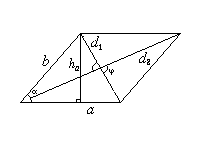
S = aha
S = ab sin 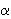
S =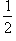 d1d2 sin
d1d2 sin 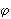
Трапеция
a и b — основания; h — расстояние между ними; l — средняя линия.
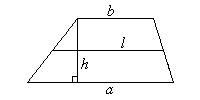
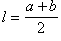
S = lh
Прямоугольник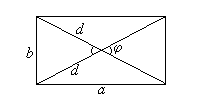
S = ab
S =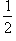 d1d2 sin
d1d2 sin 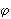
Ромб
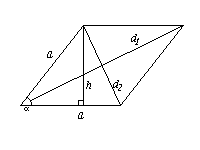
S = aha
S = a2sin 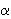
S =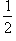 d1d2
d1d2
Квадрат
d — диагональ.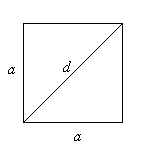
S = a2
S =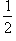 d2
d2
Планиметрия. Задачи.
Сторона треугольника равна 21, а две другие стороны образуют угол в 60o и относятся как 3:8. Найдите эти стороны.
Дан треугольник ABC . Из вершины A проведена медиана AM , а из вершины B — медиана BP . Известно, что угол APB равен углу BMA . Косинус угла ACB равен 0,8 и BP = 1 . Найдите площадь треугольника ABC .
Найдите стороны треугольника ABC, если угол А равен 45 градусов, угол С равен 30 градусов, а высота AD равна 3м.
В треугольнике ABC известно, что AB = 3, AC = 3 ,
,  ABC = 60o. Биссектриса угла ABC продолжена до пересечения в точке D с окружностью, описанной вокруг треугольника. Найдите BD.
ABC = 60o. Биссектриса угла ABC продолжена до пересечения в точке D с окружностью, описанной вокруг треугольника. Найдите BD.
Площадь треугольника АВС равна 12. На прямой АС взята точка D так, что точка С является серединой отрезка AD. Точка K — середина стороны AB, прямая KD пересекает сторону BC в точке L.
a) Докажите, что BL : LC = 2 : 1.
б) Найдите площадь треугольника BLK.
В равнобедренном треугольнике ABC AC — основание. На продолжении стороны CB за точку В отмечена точка D так, что угол CAD равен углу ABD.
а) Докажите, что AB биссектриса угла CAD.
б) Найдите длину отрезка AD, если боковая сторона треугольника АВС равна 5, а его основание равно 6.
В остроугольном треугольнике ABC проведены высоты AM и CN.
а) Докажите, что углы ACB и MNB равны.
б) Вычислите длину стороны АС, если известно, что периметр треугольника ABC равен 25 см, периметр треугольника BMN равен 15 см, а радиус окружности, описанной около треугольника BMN равен 3 см.
Площадь треугольника АВС равна 72, а сумма длин сторон АС и ВС равна 24.
а) Докажите, что треугольник АВС прямоугольный.
б) Найдите сторону квадрата, вписанного в треугольник АВС, если известно, что две вершины этого квадрата лежат на стороне АВ.
Основания трапеции равны 3 см и 5 см. Одна из диагоналей трапеции равна 8 см, угол между диагоналями равен 60o . Найдите периметр трапеции.
В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если .