Теоретический материал по теме «Окружность»
Элементы окружности
Окружность — множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости (центра окружности).
Радиусы — отрезки, соединяющие точки окружности с центром. Все радиусы данной окружности равны.
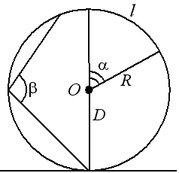
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности. Диаметр, делящий хорду пополам, перпендикулярен этой хорде
Центральный угол — угол, образованный двумя радиусами. Центральный угол измеряется дугой, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.
Длина окружности: C = 2 R, R — радиус окружности, D — диаметр.
R, R — радиус окружности, D — диаметр.
Длина дуги окружности: C= Ra = Rα/180˚ , a — радианная мера дуги, α — градусная мера.
Rα/180˚ , a — радианная мера дуги, α — градусная мера.
Круг — часть плоскости, ограниченная окружностью.
Площадь круга: S =  R² =
R² =  D²/4 .
D²/4 .
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.
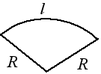
Площадь сектора:S= R²α/360˚ .
R²α/360˚ .
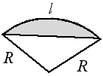
Сегмент – часть круга, ограниченная хордой и дугой.
Свойства вписанных углов
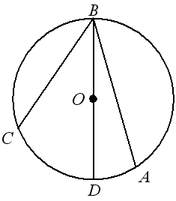
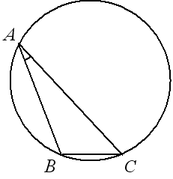
Вписанный угол измеряется половиной дуги, на которую он опирается: 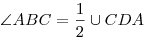 .
.
Вписанные углы, опирающиеся на одну и ту же дугу, равны: 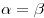 .
.
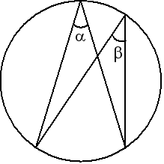
Вписанный угол, опирающийся на диаметр — прямой.
Углы, связанные с окружностью
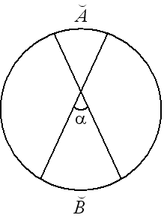
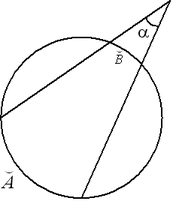
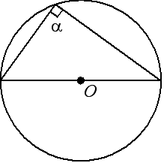
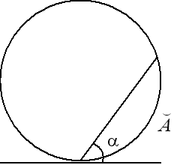
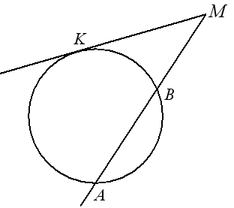
Теорема (угол между касательной и хордой, проведенной через точку касания). Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой: 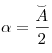 .
.
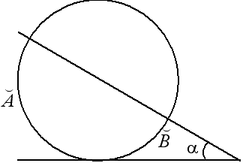
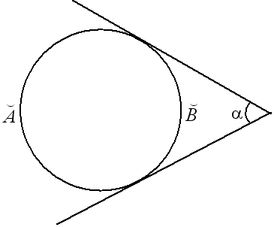
Отрезки, связанные с окружностью
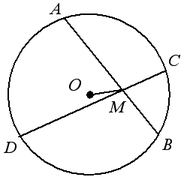
Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
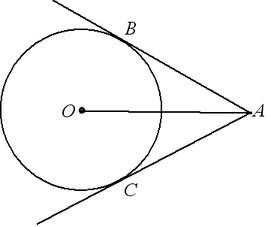
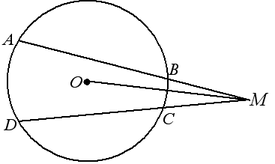
Теорема. Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равная разности квадратов радиуса окружности и расстояния от точки M до центра окружности: 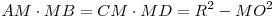 .
.
Окружность, вписанная в многоугольник
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
Теоремы:
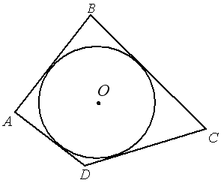
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Из параллелограммов окружность можно вписать в ромб, квадрат.
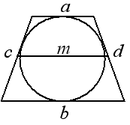
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон, а средняя линия — полусумме боковых сторон: 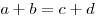 ,
, 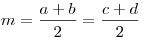 .
.
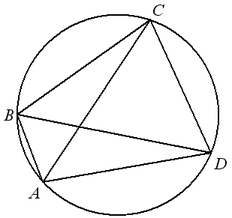
Окружность, описанная около четырехугольника
Если вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
Теоремы:
Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам.
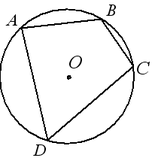
В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна 180˚.
Из всех параллелограммов окружность можно описать около прямоугольника, квадрата.
Задачи к уроку.
Две окружности внутренне касаются в точке А. Через точку А проведены две секущих этих окружностей. Одна из секущих пересекает меньшую и большую окружность в точках M и N соответственно, а другая – в точках P и Q. Доказать, что AM:AN=AP:AQ.
В круге радиуса R проведены две пересекающиеся под прямым углом хорды. Найти:
а) Сумму квадратов четырех отрезков этих хорд, на которые последние делятся точкой пересечения.
б) сумму квадратов хорд, если расстояние от центра О круга до их точки пересечения равно d.
Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.
Радиусы окружностей с центрами O1 и O2 равны соответственно 1 и 3. Найдите радиус третьей окружности, которая касается двух данных и прямой O1O2, если O1O2 = 14.
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
а) Докажите, что треугольник OLO1 прямоугольный.
б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 16.
Окружность, вписанная в треугольник ABC, касается сторон AB, BC и CA в точках K, M и N соответственно.
а) Докажите, что 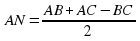
б) Найдите отношение AK : KB, если известно, что AN : NC = 4 : 3 и 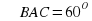 .
.
Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
В окружности проведены хорды АС и ВD, пересекающиеся в точке О, причем касательная к окружности, проходящая через точку С, параллельна BD.
а) Докажите, что 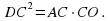
б) Найдите площадь треугольника CDO, если известно, что АВ:ВО=3:1, а площадь треугольника ACD равна 36.
В треугольнике ABC BA=8, BC=7, 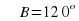 . Вписанная в треугольник окружность ω касается стороны АС в точке М.
. Вписанная в треугольник окружность ω касается стороны АС в точке М.
а) Докажите, что АМ=ВС.
б) Найдите длину отрезка с концами на сторонах АВ и АС, перпендикулярного АВ и касающегося окружности ω.
Две окружности касаются внутренним образом в точке А так, что меньшая окружность проходит через центр большей. Хорда ВС большей окружности касается меньшей в точке К. Прямые АВ и АС вторично пересекают меньшую окружность в точках Р и М соответственно.
а) Докажите, что РМ||ВС.
б) Найдите площадь треугольника АВС, если РМ=12, а радиус большей окружности равен 20.
Четырехугольник ABDC вписан в окружность. Прямые АВ и CD пересекаются в точке Р.
а) Докажите, что 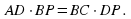
б) Найдите площадь треугольника APC, если известно, что 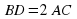 , а площадь четырехугольника ABDC равна 36.
, а площадь четырехугольника ABDC равна 36.









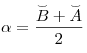 .
.
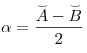 .
.
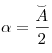 .
.











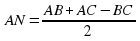
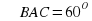 .
.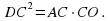
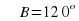 . Вписанная в треугольник окружность ω касается стороны АС в точке М.
. Вписанная в треугольник окружность ω касается стороны АС в точке М.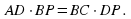
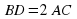 , а площадь четырехугольника
, а площадь четырехугольника