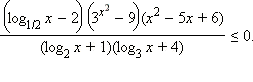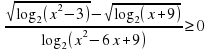Задача 15 (С3). Логарифмические неравенства.
На занятии мы рассмотрим особенности решения логарифмических неравенств, тонкости употребления определения логарифма и логарифмической функции.
.
Конспект занятия "Задача 15 (С3). Логарифмические неравенства."
Задания по теме для самостоятельного решения
Задание 1
(2 балла)Решите неравенство . В ответ запишите длину промежутка решения.
Задание 2
(3 балла)Решите неравенство В ответе укажите модуль суммы целых решений неравенства.
Задание 3
(3 балла)Решите неравенство . В ответе укажите наименьшее целое решение.


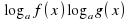 эквивалентно системе:
эквивалентно системе: 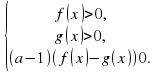
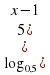 .
.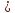
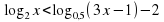 .
.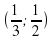
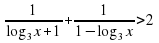 .
. 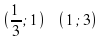
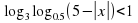 .
.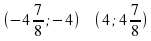
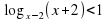 .
. 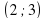
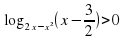 .
. 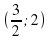
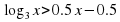 .
.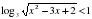 .
.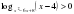
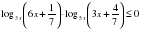 .
.