Конспект занятия "Задача 14 (С2). Стереометрия. Расстояния и углы в пространстве."
Файл к уроку 25
Координатный метод. Нахождение расстояний и углов в пространстве.
Как и на плоскости, в пространстве мы можем вводить систему координат, и в этой системе находить координаты точек, уравнения прямых и плоскостей, а зная их – вычислять расстояния и углы в пространстве, используя координатный метод.
Уравнение прямой в пространстве определяется точкой 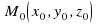 на прямой и направляющим вектором
на прямой и направляющим вектором 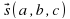 :
: 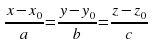 (оно же каноническое уравнение).
(оно же каноническое уравнение).
Уравнение прямой, проходящей через 2 точки 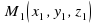 и
и 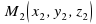 :
: 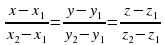 .
.
Уравнение прямой можно задать и как пересечение двух плоскостей: 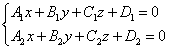
Соответственно уравнение плоскости в пространстве имеет вид: 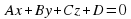 , где
, где 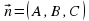 – нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
– нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
Угол между прямыми в пространстве:

Точка К – середина ребра АA1 куба АВСDA1B1C1D1. Найдите угол между прямыми A1В и СК.
В правильной шестиугольной призме все ребра равны 1. Найдите косинус угла между прямыми АВ1 и ВF1
Угол между прямой и плоскостью
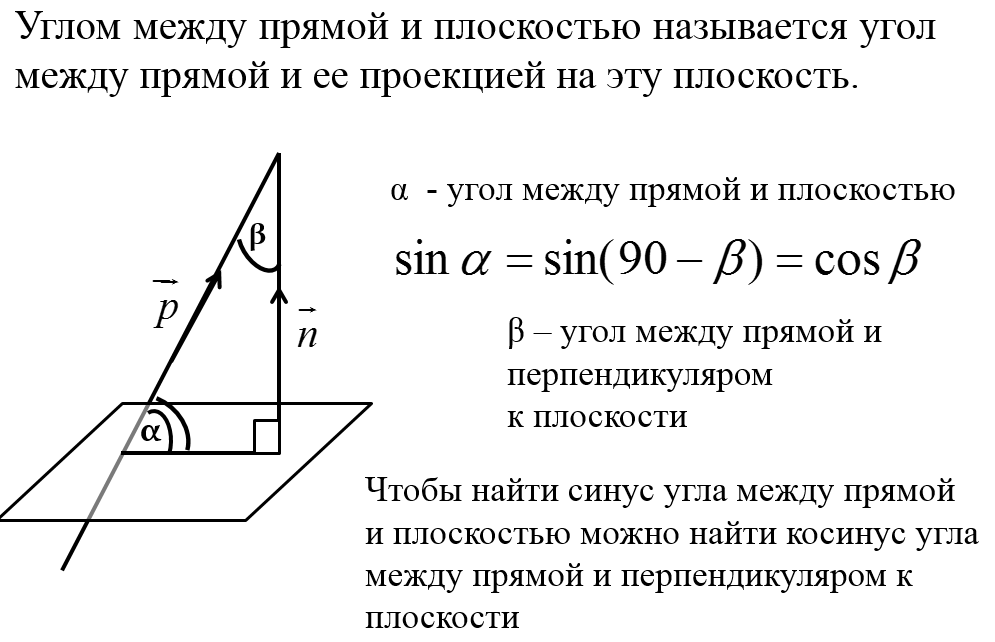

В единичном кубе найдите угол между прямой AВ1 и плоскостью (А1EF), где Е – середина В1С1, BF = 1/3BB1.
Угол между плоскостями

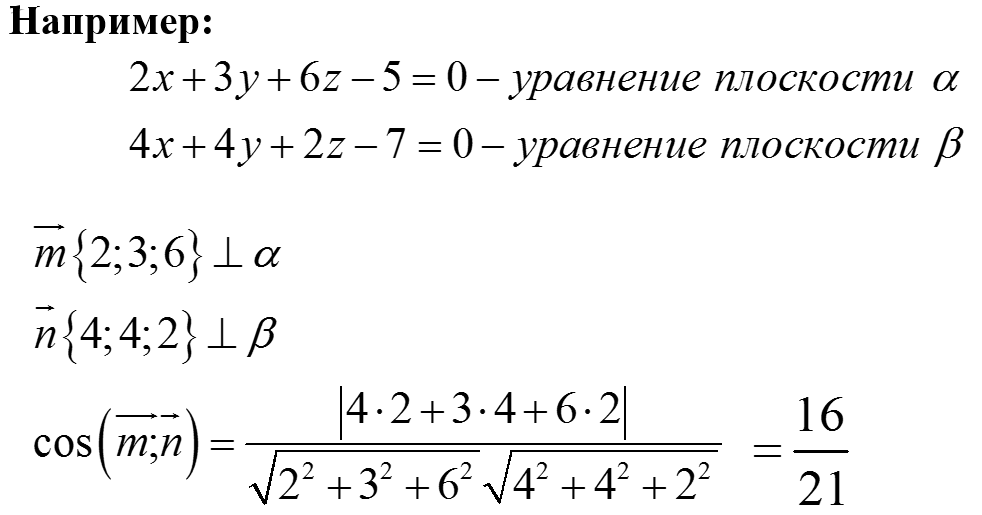
В правильной треугольной призме все ребра равны 1. Найдите угол между плоскостями (АВС1) и (А1В1С).
Расстояние между двумя точками 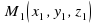 и
и 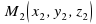 можно вычислить по формуле:
можно вычислить по формуле: 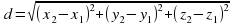
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.

Итак, для того, чтобы найти расстояние от точки до плоскости нам необходимо найти координаты точки, и координаты нормали данной плоскости. После чего воспользоваться следующей формулой:




В кубе АВСDA1B1C1D1 проведена диагональ B1D. В каком отношении, считая от вершины B1, плоскость А1BC1 делит диагональ B1D?
Дан прямоугольный параллелепипед ABCDA1B1C1D1, у которого АВ = 3, АD = 2 и AA1 = 7 единиц. Точка E лежит на ребре АА1 и делит его в отношении 5 : 2считая от точки А. Найдите угол между скрещивающимися прямыми ВЕ и А1С.
Основание прямой четырехугольной призмы ABCDA1B1C1D1 – прямоугольник ABCD, в котором AB = 5, 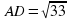 . Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно
. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно 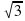 .
.
В кубе ABCDA1B1C1D1 точка Е – середина ребра А1В1. Найдите синус угла между прямой АЕ и плоскостью BDD1.
В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит прямоугольник ABCD со сторонами 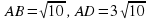 . Высота параллелепипеда
. Высота параллелепипеда 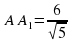 . Найдите расстояние от точки А до плоскости A1DB.
. Найдите расстояние от точки А до плоскости A1DB.
Дана правильная призма ABCA1B1C1, у которой стороны основания AB = 4, а боковое ребро АА1 = 9. Точка М – середина ребра АС, а на ребре АА1 взята точка Т так, что АТ = 5.
а) докажите, что ВВ1М делит отрезок С1Т пополам.
б) Плоскость ВТС1 делит отрезок МВ1на две части. Найти длину меньшей из них. Заполнить пропуски в решении.


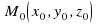 на прямой и направляющим вектором
на прямой и направляющим вектором 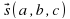 :
: 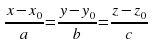 (оно же каноническое уравнение).
(оно же каноническое уравнение).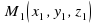 и
и 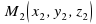 :
: 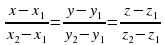 .
.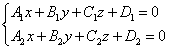
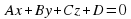 , где
, где 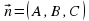 – нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
– нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.



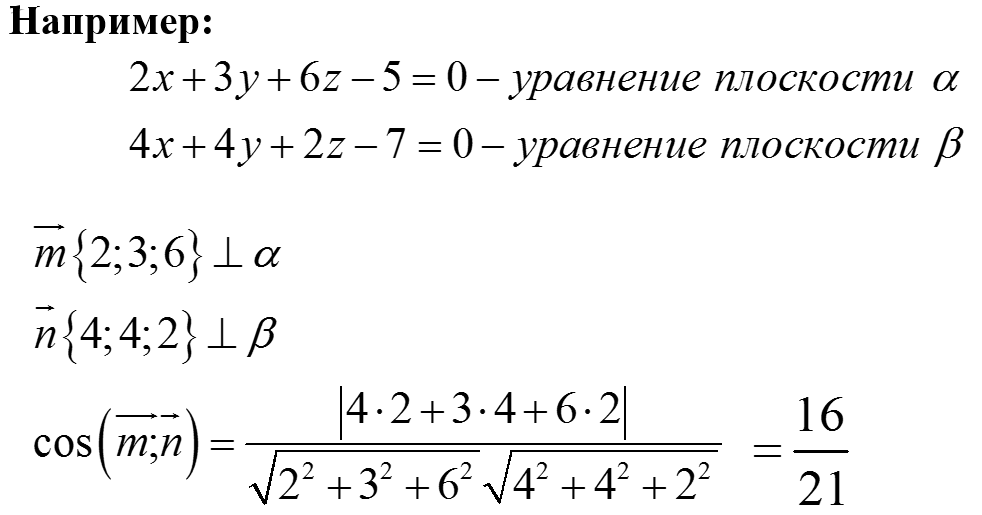
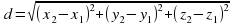


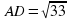 . Найдите тангенс угла между плоскостью грани
. Найдите тангенс угла между плоскостью грани 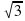 .
.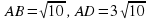 . Высота параллелепипеда
. Высота параллелепипеда 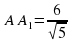 . Найдите расстояние от точки А до плоскости
. Найдите расстояние от точки А до плоскости