Конспект занятия "Задача 14 (С2). Стереометрия. Многогранники и тела вращения."
Файл к уроку 26
Координатный метод.
Сегодня мы продолжим разговор о координатном методе и посмотрим, как применять его при вычислении площадей сечений и объемов многогранников, решим задачи ЕГЭ 2016 года, используя данный метод.
Основные формулы остаются теми же, но с ними понадобятся и формулы площади многоугольников.
Уравнение прямой в пространстве определяется точкой 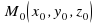 на прямой и направляющим вектором
на прямой и направляющим вектором 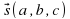 :
: 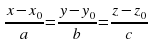 (оно же каноническое уравнение).
(оно же каноническое уравнение).
Уравнение прямой, проходящей через 2 точки 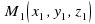 и
и 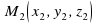 :
: 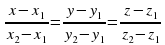 .
.
Уравнение прямой можно задать и как пересечение двух плоскостей: 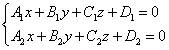
Соответственно уравнение плоскости в пространстве имеет вид: 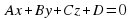 , где
, где 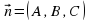 – нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
– нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
Угол между прямыми в пространстве – угол между их направляющими векторами:
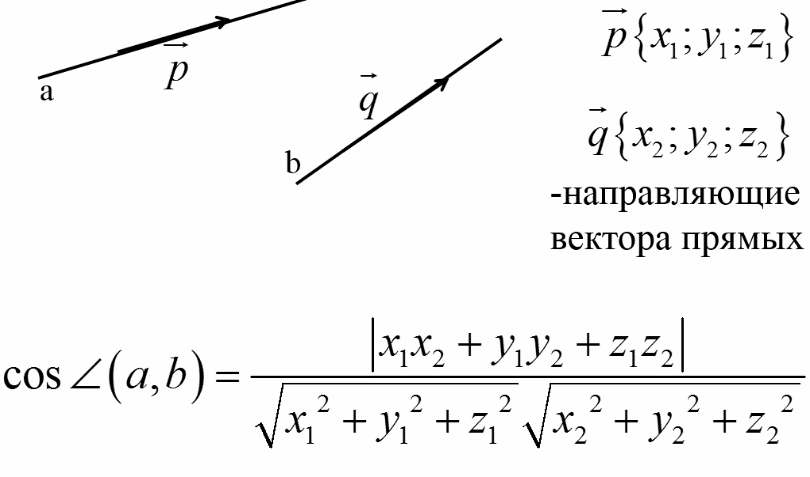
Угол между прямой и плоскостью:
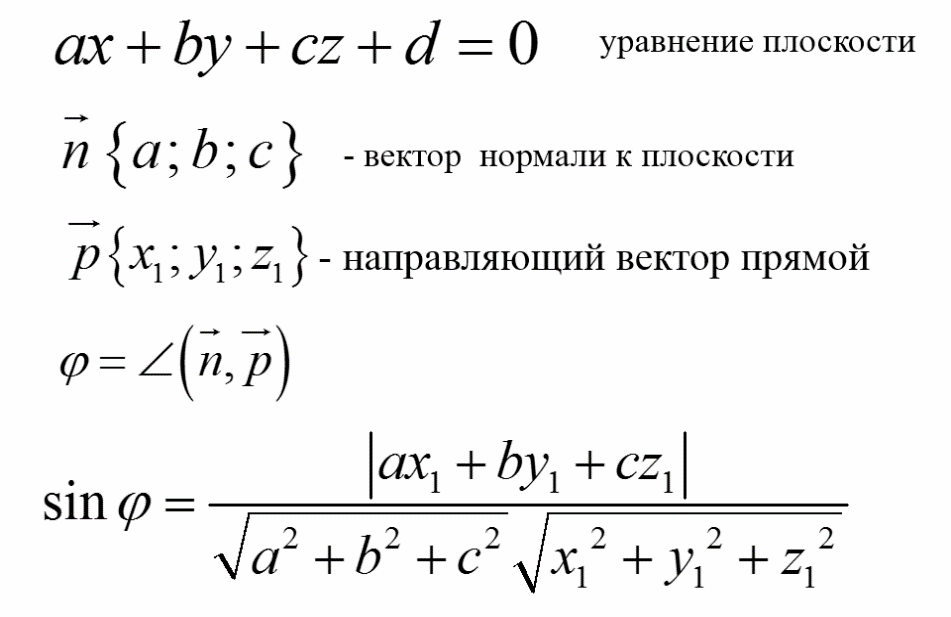
Угол между плоскостями

Расстояние между двумя точками 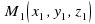 и
и 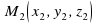 можно вычислить по формуле:
можно вычислить по формуле: 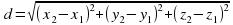
Расстояние от точки М до плоскости α, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.



Задачи к уроку:
Точка E — середина ребра BB1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью D1AE, если ребра куба равны 4.
Правильные треугольники ABC и ABM лежат в перпендикулярных плоскостях, 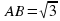 . Точка P — середина AM, а точка T делит отрезок BM так, что BT : TM = 3 : 1. Вычислите объём пирамиды MPTC.
. Точка P — середина AM, а точка T делит отрезок BM так, что BT : TM = 3 : 1. Вычислите объём пирамиды MPTC.
В правильной треугольной призме АВСА1В1С1 сторона основания АВ равна 6, а боковое ребро АА1 равно 3. На ребре АВ отмечена точка К так, что АК = 1. Точки М и L — середины рёбер А1С1 и В1С1 соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости γ;
б) Найдите расстояние от точки С до плоскости γ.
В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA = 6. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM — точка L. Известно, что AD = AL = 2, и BE = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно 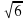 . На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
. На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL - квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Дана правильная призма ABCA1B1C1, у которой стороны основания AB = 4, а боковое ребро АА1 = 9. Точка М – середина ребра АС, а на ребре АА1 взята точка Т так, что АТ = 5.
а) докажите, что ВВ1М делит отрезок С1Т пополам.
б) Плоскость ВТС1 делит отрезок МВ1на две части. Найти длину меньшей из них.


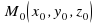 на прямой и направляющим вектором
на прямой и направляющим вектором 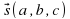 :
: 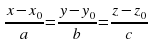 (оно же каноническое уравнение).
(оно же каноническое уравнение).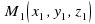 и
и 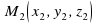 :
: 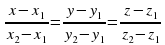 .
.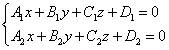
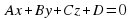 , где
, где 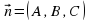 – нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.
– нормальный (перпендикулярный) вектор плоскости. Для определения положения плоскости в пространстве достаточно знать 3 точки, через которые она проходит, не лежащие на одной прямой.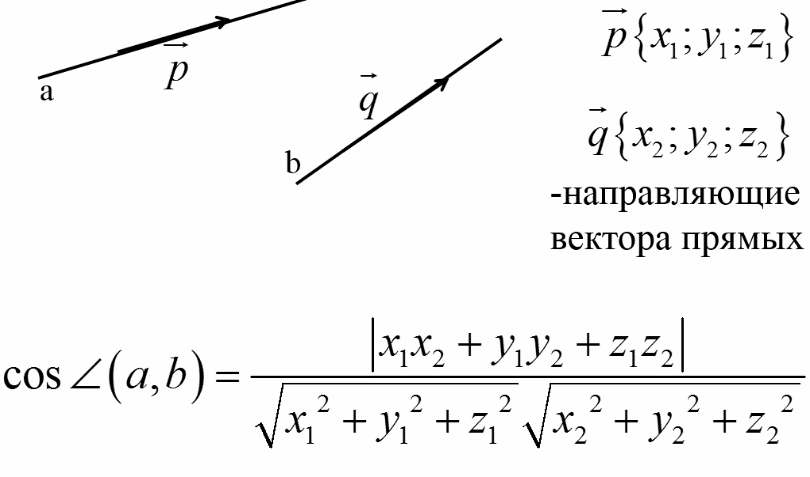
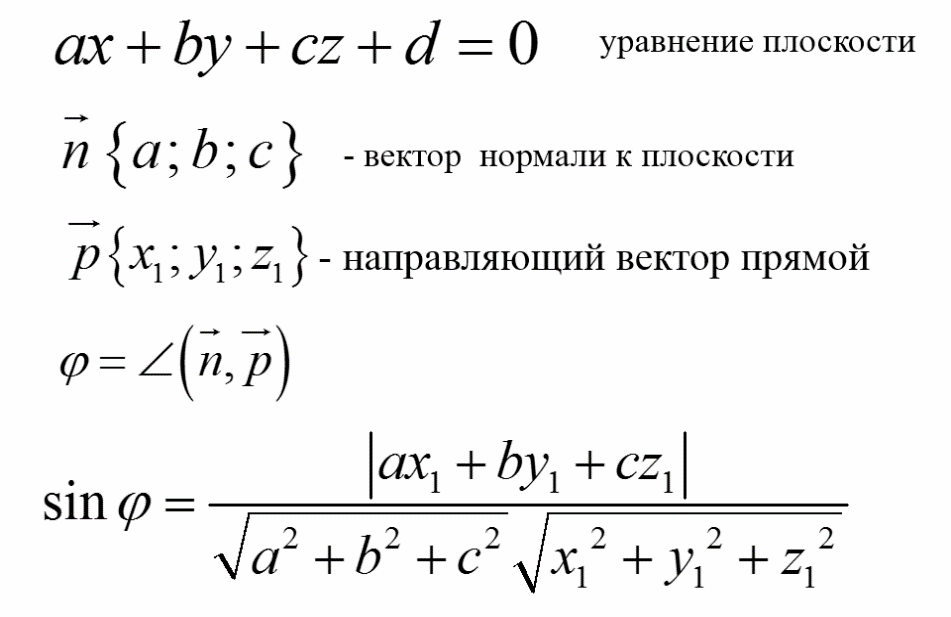

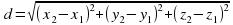


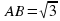
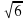 . На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
. На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.