Многогранники. Призма, пирамида.

Многогранники

Призма

Призмой называется многогранник, две грани которого n-угольники, а остальные n граней — параллелограммы.Боковые ребра призмы равны и параллельны.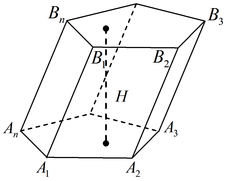

Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.Поверхность призмы состоит из оснований и боковой поверхности призмы. Боковая поверхность призмы состоит из параллелограммов.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. В противном случае призма называется наклонной.

У прямой призмы боковые грани – прямоугольники.

Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если она прямая, и ее основания — правильные многоугольники

Площадь поверхности и объём призмы

Пусть H — высота призмы, 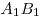 — боковое ребро призмы,  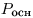— периметр основания призмы,  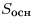площадь основания призмы,  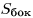— площадь боковой поверхности призмы,  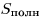— площадь полной поверхности призмы,  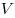- объем призмы,  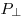— периметр перпендикулярного сечения призмы,  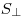— площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

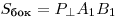
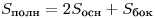
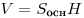
Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований, площадь боковой поверхности и объем даются формулами:

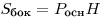
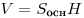
Параллелепипед

Параллелепипедом называется призма, основанием которой является параллелограмм.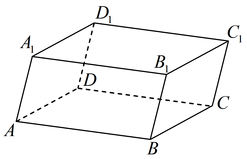

Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда все грани — параллелограммы.

Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда.

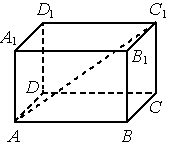
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.

Длины не параллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три линейных размера.

Свойства параллелепипеда:

 Противоположные грани параллелепипеда равны и параллельны.

 Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

 Боковые грани прямого параллелепипеда — прямоугольники.

 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Пирамида

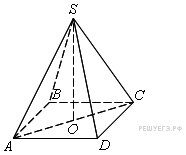
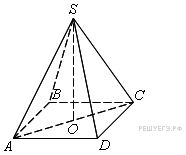
Пирамидой называется многогранник одна из граней которого является произвольным многоугольником, а остальные грани — треугольники, имеющие общую вершину.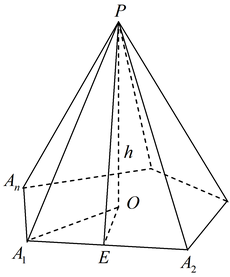

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды.

Тетраэдр — это пирамида, в основании которой лежит треугольник.

Треугольники, из которых состоит тетраэдр, называются его гранями, их стороны — ребрами, а вершины — вершинами тетраэдра. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. Обычно выделяют одну из граней тетраэдра и называют ее основанием, а остальные грани называют боковыми гранями.

Правильным тетраэдром называют тетраэдр, у которого все ребра равны.

Правильной пирамидой называется такая пирамида, основание которой— правильный многоугольник, а основание высоты пирамиды совпадает с центром этого многоугольника. Прямая, содержащая высоту правильной пирамиды, называется ее осью.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

Свойства правильной пирамиды:

1. Боковые ребра пирамиды равны.

2. Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.

3. Вершина пирамиды проектируется в центр окружности, описанной около основания пирамиды.

4. Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны, а высота пирамиды лежит внутри пирамиды.

5. Все двугранные углы при основании пирамиды равны.

6. Вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды.

7. В правильной треугольной пирамиде противоположные ребра попарно перпендикулярны.

Замечание:

1. Если боковые ребра пирамиды равны между собой, то в основании лежит правильный многоугольник, вокруг которого можно описать окружность, а вершина пирамиды проецируется в центр этой окружности.

2. Если двугранные углы при основании пирамиды равны между собой, то в основании пирамиды лежит многоугольник, в который можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.

Площадь поверхности и объём пирамиды

Пусть 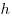 — высота пирамиды,  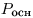— периметр основания пирамиды,  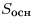— площадь основания пирамиды,  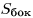— площадь боковой поверхности пирамиды,  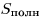— площадь полной поверхности пирамиды,  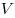— объем пирамиды. Тогда имеют место следующие соотношения:

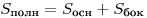
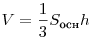
Если все двугранные углы при основании пирамиды равны 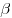, а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны 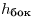, то

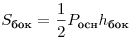
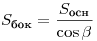
Правильные многогранники

Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер.

Все ребра правильного многогранника равны, все двугранные углы правильного многогранника равны, все многогранные углы правильного многогранника равны. Существует ровно пять выпуклых правильных многогранников:

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, и в каждой вершине многогранника сходится одно и то же число ребер.

Все ребра правильного многогранника равны друг другу. Равны также все его двугранные углы, содержащие две грани с общим ребром.

Грани правильного многогранника могут быть либо равносторонними треугольниками, либо квадратами, либо правильными пятиугольниками. Действительно, угол правильного 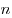-угольника при 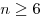не меньше 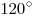. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при 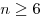, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 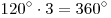. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше .

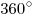По этой же причине каждая вершина правильного многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников. Других возможностей нет.

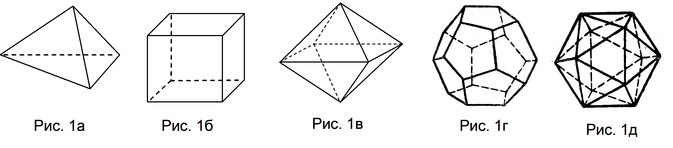
• Правильный тетраэдр (четырехгранник) — многогранник, составленный из четырех правильных треугольников (рис.1а).

• Правильный гексаэдр (шестигранник) или куб — многогранник, составленный из шести правильных четырехугольников (квадратов) (рис. 1б).

• Правильный октаэдр (восьмигранник) — многогранник, составленный из восьми правильных треугольников (рис. 1в).

• Правильный додекаэдр (двенадцатигранник) — многогранник, составленный из двенадцати правильных пятиугольников (рис. 1г).

• Правильный икосаэдр (двадцатигранник) — многогранник, составленный из двадцати правильных треугольников (рис. 1д).