Принцип Дирихле. Правило крайнего. Подсчет двумя способами.

Принцип Дирихле.

Утверждение «среди любых трех целых чисел найдутся два числа одной четности» кажется очевидным, также как и утверждение «среди 13 человек найдутся двое, родившиеся в один месяц». И то, и другое можно обосновать разбором случаев. Но более грамотным будет построить рассуждение от противного. Для второго утверждения это будет выглядеть так:

«Предположим, что не найдется двух таких человек. Тогда в каждый из 12 месяцев родилось не более одного человека. Значит, имеется всего не более 12 человек, что противоречит условию задачи: 12

Такие рассуждения очень часто встречаются при решении задач, поэтому их выделили в отдельное утверждение, называемое принципом Дирихле. Классическая формулировка звучит так: «Если (n + 1) кроликов сидят в n ящиках, то найдётся ящик, в котором сидит, по крайней мере, два кролика». Доказательство этого утверждения также строится от противного:

«Предположим, что в каждом ящике сидит менее двух кроликов (один или ни одного). Тогда во всех n ящиках в совокупности сидит не более n кроликов. Противоречие.»

Решение задачи с помощью принципа Дирихле сводится к выбору «кроликов» и «клеток». Иногда не совсем очевидно, кто в данной задаче является «кроликом», и что служит «клеткой».

1. Обязательно ли среди двадцати пяти "медных" монет (т.е. монет достоинством 1, 2, 3, 5 коп.) найдётся семь монет одинакового достоинства?

2. а) Докажите, что в любой футбольной команде есть два игрока, которые родились в один и тот же день недели.

b) Докажите, что среди жителей Москвы найдутся десять тысяч, празднующих день рождения в один и тот же день.

1. В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них заведомо оказались два шарика одного цвета?

2. Дано 12 целых чисел. Докажите, что из них можно вы­брать 2, разность которых делится на 11.

3. В ковре размером 4x4 метра моль проела 15 дырок. До­кажите, что из него можно вырезать коврик размером 1x1 метр, не содержащий внутри себя дырок. (Дырки можно счи­тать точечными).

4. В классе учатся 38 человек. Докажите, что среди них найдутся четверо, родившихся в один месяц.

5. В поход пошли 20 туристов. Самому старшему из них 35 лет, а самому младшему 20 лет. Верно ли, что среди туристов есть одногодки?

6. Докажите, что из 52 целых чисел всегда найдутся два, разность квадратов которых делится на 100.

7. Сто человек сидят за круглым столом, причем более половины из них - мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга.

8. У Пети в кармане несколько монет. Если Петя наугад вытащит из кармана 3 монеты, среди них обязательно найдётся монета "1 рубль". Если Петя наугад вытащит 4 монеты из кармана, среди них обязательно найдётся монета "2 рубля". Петя вытащил из кармана 5 монет. Назовите эти монеты.

9. Дано 8 различных натуральных чисел, не больших 15. Докажите, что среди их положительных попарных разностей есть три одинаковых.

Подсчет двумя способами

В некоторых задачах можно получить нужное уравнение, если вычислить двумя способами одну и ту же величину. Трудность состоит в том, чтобы додуматься — какую именно величину подсчитывать двумя способами.

1. Можно ли в прямоугольной таблице 5×10 так расставить числа, чтобы сумма чисел каждой строки равнялась бы 30, а сумма чисел каждого столбца равнялась бы 10?

2. Дано 25 чисел. Какие бы три из них мы ни выбрали, среди оставшихся найдётся такое четвёртое, что сумма этих четырёх чисел будет положительна. Верно ли, что сумма всех чисел положительна?

3. Рита, Люба и Варя решали задачи. Чтобы дело шло быстрее, они купили конфет и условились, что за каждую решённую задачу девочка, решившая её первой, получает четыре конфеты, решившая второй  — две, а решившая последней  — одну. Девочки говорят, что каждая из них решила все задачи и получила 20 конфет, причём одновременных решений не было. Они ошибаются. Как вы думаете, почему?

4. Ковровая дорожка покрывает лестницу из 9 ступенек. Длина и высота лестницы равны 2 метрам. Хватит ли этой ковровой дорожки, чтобы покрыть лестницу из 10 ступенек длиной и высотой 2 метра?

5. Несколько шестиклассников и семиклассников обменялись рукопожатиями. при этом оказалось, что каждый шестиклассник пожал руку семи семиклассникам, а каждый семиклассник пожал руку шести шестиклассникам. Кого было больше - шестиклассников или семиклассников?

6. В сказочной стране Перра-Терра среди прочих обитателей проживают Карабасы и Барабасы. Каждый Карабас знаком с шестью Карабасами и девятью Барабасами. Каждый Барабас знаком с десятью Карабасами и семью Барабасами. Кого в этой стране больше – Карабасов или Барабасов?

7. 10 друзей послали друг другу праздничные открытки, так что каждый послал 5 открыток. Докажите, что найдутся двое, которые послали открытки друг другу.

8. Можно ли в клетки квадрата 10×10 поставить некоторое количество звёздочек так, чтобы в каждом квадрате 2×2 было ровно две звёздочки, а в каждом прямоугольнике 3×1 – ровно одна звёздочка? (В каждой клетке может стоять не более одной звёздочки.)

9. Когда встречаются два жителя Цветочного города, один отдает другому монету в 10 копеек, а тот ему - 2 монеты по 5 копеек. Могло ли случиться так, что за день каждый из 1990 жителей города отдал ровно 10 монет?

10. Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и чёрных пятиугольников. Каждый чёрный лоскут граничит только с белыми, а каждый белый — с тремя чёрными и тремя белыми. Сколько лоскутков белого цвета?

11. Каждый участник двухдневной олимпиады в первый день решил столько же задач, сколько все остальные в сумме – во второй день. 
    Докажите, что все участники решили поровну задач.

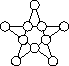
12. Можно ли в кружочки на пятиконечной звезде (см. рисунок) расставить 4 единицы, 3 двойки и 3 тройки так, чтобы суммы четырех чисел, стоящих на каждой из пяти прямых, были равны? 
    
    
    

Правило крайнего

Правило «крайнего» может быть кратко выражено словами «Рассмотри крайнее!». Это правило есть попросту рекомендация рассмотреть объект, обладающий какими-либо «крайними», или, как говорят математики, экстремальными свойствами. Например, наибольшую или наименьшую площадь, наибольшую или наименьшую сторону треугольника, наибольший или наименьший угол треугольника. Если речь в задаче идет о множестве точек на прямой, то правило «Рассмотри крайнее!» советует сосредоточить свое внимание на самой крайней точке множества (самой левой или самой правой). Если в задаче фигурирует некоторый набор чисел, то правило «крайнего» рекомендует рассмотреть наибольшее или наименьшее из этих чисел.

Примеры задач, решаемых данным методом.

1. На полях бесконечной шахматной доски написаны натуральные числа так, что каждое число равно среднему арифметическому четырех соседних чисел – верхнего, нижнего, правого и левого. Докажите, что все числа на доске равны между собой.

2. На плоскости отмечено конечное множество точек. Известно, что площадь произвольного треугольника с вершинами в трех из данных точек не больше единицы. Доказать, что все данные точки можно накрыть треугольником площади 4.

3. Семеро ребят вместе собрали 100 грибов, причем количество грибов у любых двоих из грибников различно. Докажите, что найдутся трое ребят, собравших вместе не менее 50 грибов.