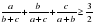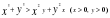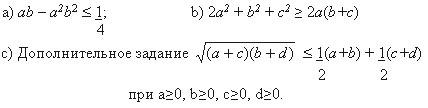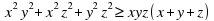Конспект занятия "Неравенства. Доказательства неравенств. Задачи олимпиад"
Неравенства. Свойства неравенств. Задачи олимпиад.
Определение: Говорят, что действительное число a больше (меньше) действительного числа b, если их разность a-b –положительное (отрицательное) число.
Свойства:
Если ab и bc, то ac.
Если ab , то a+cb+c.
Если ab и m0, то ambm.
Если ab и mambm.
Если ab и bc, то ac.
Если ab и cd, то a+cb+d.
Если ab и cd, то acbd, a,b,c,d0.
Если ab , то anbn ,a,b  0,
0,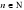 .
.
Если ab , то anbn ,n-нечетное.
Провести доказательства некоторых свойств.
Классические неравенства:
1) 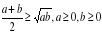 (неравенство Коши)
(неравенство Коши)
2) 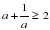
Историческая справка:
Неравенство (1) называют в честь французского математика Огюста Коши. Число 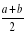 называют средним арифметическим чисел a и b;
называют средним арифметическим чисел a и b;
число 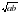 называют средним геометрическим чисел a и b. Таким образом, неравенство означает, что среднее арифметическое двух положительных чисел не меньше их среднего геометрического.
называют средним геометрическим чисел a и b. Таким образом, неравенство означает, что среднее арифметическое двух положительных чисел не меньше их среднего геометрического.
ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ
Задачи на доказательство неравенств часто встречаются на математических турнирах разного уровня. Мы собрали несколько интересных и посильных 8-му классу приемов доказательства.
Некоторые приемы доказательства неравенств.
1. Использование определения понятий «больше» и «меньше» (т. е. рассмотрение разности между левой и правой частями неравенства).
Пример 1. Доказать неравенство Коши: 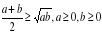
Решение. Рассмотрим разность
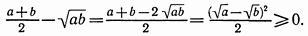
Следовательно, исходное неравенство верно.
Это неравенство означает, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического, причем равенство достигается только в том случае, когда a=b.
2. Использование известных неравенств.
Пример 2. Доказать, что 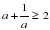 для любого положительного a .
для любого положительного a .
УПРАЖНЕНИЯ
Доказательство неравенств с использованием определения понятия неравенства.
1. Доказать неравенство 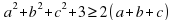
2. Доказать, что при любых значениях x и y верно неравенство
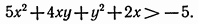
Доказательство неравенств путем преобразования очевидного или известного классического неравенства к виду доказываемого неравенства.
3. Доказать неравенство
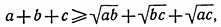
если a, b, c — неотрицательные числа.
4. Доказать, что
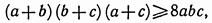
если a,b,c — неотрицательные числа.
5. Доказать неравенство: ab(a+b)+bc(b+c)+ac(a+c)  6abc
6abc
6. .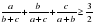
7. Доказать неравенство: 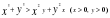
8. Докажем, что (a+b)(ab+1) 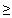 4ab, при а
4ab, при а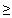 0, b
0, b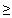 0.
0.
9. Доказать неравенство: 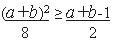
10. Докажите неравенства:
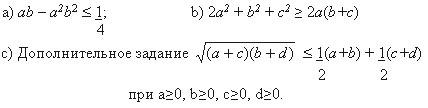
11. Докажите справедливость неравенства:
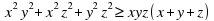

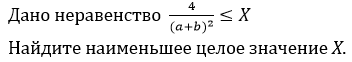




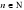 .
.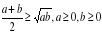 (неравенство Коши)
(неравенство Коши)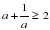
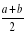 называют средним арифметическим чисел
называют средним арифметическим чисел 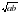 называют средним геометрическим чисел
называют средним геометрическим чисел 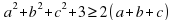
 6
6