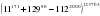Файл к уроку 8-9 класс
Делимость. Основная теорема арифметики. Деление с остатком. Сравнение по модулю.
Сегодня на занятии мы поговорим о натуральных числах, вспомним, что такое простые и составные числа, делители числа, и поработаем с основной теоремой арифметики.
Говорят, что число а делится на b (или говорят, что число b делитель числа a), если существует число с такое, что а=bc.
Простые числа – числа, имеющие ровно 2 делителя.
Составные числа – числа, имеющие больше двух делителей.
Взаимно простые числа – числа, не имеющие общих простых делителей, то есть НОД их равен 1.
Алгоритм нахождения НОД, не используя разложения чисел на простые множители, называют Алгоритм Евклида/ Он состоит в последовательном применении правила: НОД (a, b)= НОД (a-b, b).
Пример: Докажите, что дробь 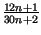 - несократима ни при каком натуральном n.
- несократима ни при каком натуральном n.
Дробь не сократима, значит НОД числителя и знаменателя равен 1. Найдем возможные значения НОД (30n+2, 12n+1)=НОД (6n, 12n+1)= НОД (6n, 1) = 1.
Основная теорема арифметики: любое натуральное число единственным образом представимо в виде произведения степеней простых чисел 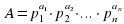 .
.
Если число 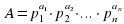 , то количество натуральных делителей числа можно вычислить по формуле
, то количество натуральных делителей числа можно вычислить по формуле 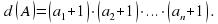
Пример: Найдите количество натуральных делителей числа 84.
Решение.
Разложим 84 на простые множители:

Таким образом, каноническое разложение имеет вид 84=22·3·7. Тогда число натуральных делителей равно (2+1)·(1+1)·(1+1)=12.
Существует ли натуральное число, произведение цифр которого равно 1365?
Сколько существует целых чисел от 1 до 16500, которые
а) не делятся на 5;
б) не делятся ни на 5, ни на 3;
в) не делятся ни на 5, ни на 3, ни на 11?
Ваня задумал простое трёхзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух?
Найдите все простые числа p и q, для которых выполняется равенство p2 – 2q2 = 1.
Найдите все натуральные n 1, для которых n3 – 3 делится на n – 1.
Сумма двух целых чисел равна 101, а разность их квадратов – простое число. Найдите эти числа.
Произведение двух натуральных чисел, каждое из которых не делится нацело на 10, равно 1000. Найдите их сумму.
Тема: Деление с остатком.
Если число a при делении на b в частном дает q и остаток r, то это можем записать как a = bq + r, где 0 ≤ r b. (Например, 26 при делении на 3 в частном даст 8 и остаток 2: 26 = 3×8 + 2)
Если от некоторого трехзначного числа отнять 6, то оно разделится на 7, если отнять 7, то оно разделится на 8, а если отнять 8, то оно разделится на 9. Определите это число.
Докажите, что если a и 5a имеют одинаковую сумму цифр, то a делится на 9.
Работа с остатками важна не только для вычисления неких недостающих чисел, но и для доказательства утверждений о делимости. Рассмотрим следующие примеры:
Доказать, что если р и р2+2 – простые числа, то и р3+4 – тоже простое.
Докажите, что а2- а четно при любом целом а.
Оказывается справедливо такое утверждение: если р - простое число, то аp- а кратно р при любом целом а.
Это утверждение имеет своё имя - «малая теорема Ферма». Она была открыта советником парламента Тулузы (Франция) Пьером Ферма в 1640 году.
Задача 11 является частным случаем этой теоремы (р=2);
Сформулируем и докажем теорему для р=3 и р=5.
Докажите, что а3- а кратно 3 при любом целом а.
Докажите, что а5 - а делится на 5 при любом целом а.
Докажите, что если a нечётно, то a2 – 1 делится на 8.
Докажите, что, каковы бы ни были целые числа a и b , число
ab(a2 – b2)(4a2 – b2) всегда делится на 5.
Докажите, что при любом целом n число n(2n + 1)(7n + 1) делится на 6.
Докажите, что каковы бы ни были целые числа a, b, с, число a2 + b2 + с2 + 1 не делится на 8.
Докажите, что если a и b – нечётные числа, то a2 - b2 делится на 8.
Когда речь заходит об остатках, можно применять сравнение по модулю.
Два натуральных числа a и b, разность которых кратна натуральному числу m, называются сравнимыми по модулю m:
a ≡ b (mod m).
Или говорят, a ≡ b (mod m), если а и b дают одинаковые остатки при делении на m.
Свойства сравнений:
Пусть a ≡ b (mod m), c ≡ d (mod m). Тогда:
a + c ≡ b + d (mod m),
a – c ≡ b – d (mod m),
ac ≡ bd (mod m).
Пусть ab ≡ 0 (mod m), и числа a и m взаимно просты. Тогда b ≡ 0 (mod m).
Пример: Доказать свойство делимости на 9: число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.
Решение.
Произвольное число 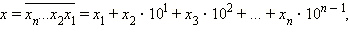 где
где 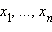 – цифры числа x в десятичной записи. Так как 10 ≡ 1 (mod 9), то 102 ≡ 1 (mod 9) и вообще 10k ≡ 1 (mod 9) для любого натурального k. Отсюда
– цифры числа x в десятичной записи. Так как 10 ≡ 1 (mod 9), то 102 ≡ 1 (mod 9) и вообще 10k ≡ 1 (mod 9) для любого натурального k. Отсюда
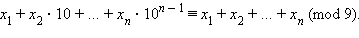
Теорема доказана.
Пример: Свойство делимости на 19. Доказать, что число делится без остатка на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.
Для любого натурального x верно равенство x = x1 + 10x2, где x1 – число единиц, x2 – число десятков этого числа. Пусть y = x2 + 2x1(то есть y – число десятков, сложенное с удвоенным числом единиц). Тогда 10y – x = 19x1 ≡ 0 (mod 19), откуда следует, что x ≡ 0 (mod 19) тогда и только тогда, когда 10y ≡ 0 (mod 19), то есть y ≡ 0 (mod 19). Утверждение доказано.
Доказать, что число 3099+61100 делится на 31.
У числа 22016 находят сумму цифр, у нового числа также находят сумму его цифр, и так до тех пор, пока число не станет однозначным. Какое число получат в конце?
Сравнение по модулю.
Доказать, что 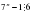 для любого натурального n.
для любого натурального n.
Доказать, что 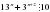 для любого натурального n.
для любого натурального n.
Доказать, что 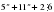 для любого нечетного n.
для любого нечетного n.
Найдите остаток от деления на 5 числа 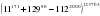


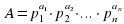 .
.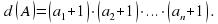

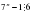 для любого натурального
для любого натурального 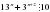 для любого натурального
для любого натурального 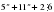 для любого нечетного
для любого нечетного