Конспект занятия "Задача 19 (С6). Задачи вида «Оценка + пример»."
Задачи вида «Оценка + пример»
Оценка плюс пример — это метод решения задач, который применяется при нахождении наибольших или наименьших значений. Суть метода состоит в следующем. Предположим, что мы ищем наименьшее значение некоторой величины A. Действуем в два этапа:
Оценка. Показываем, что выполнено неравенство A⩾α
Пример. Предъявляем пример, когда достигается равенство A=α.
Тем самым доказываем, что наименьшее значение величины A равно α.
Суть этого рассуждения лучше всего уяснить на конкретных примерах
Найдите наибольшее значение функции f(x)=-x2+2x-7
Решение: выделим полный квадрат: f(x)=-x2+2x-7=-(x2-2x+1)-6=-(х-1)2-6≤-6
Так как полный квадрат неотрицателен, а с минусом впереди – не положителен, то наибольшее значение функции равно -6 и достигается оно при х=1, f(1)=-6.
Ответ: -6.
Каково наименьшее натуральное n такое, что n! делится на 18, на 19, на 20 и на 21?
Решение: Заметим, что число 19 — простое, поэтому если n, то n! не делится на 19. Осталось понять, что 19! делится и на 18, и на 19, и на 20 (20=4⋅5), и на 21 (21=3⋅7).
Ответ: 19.
Каким наименьшим числом монет в 3 и 5 копеек можно набрать сумму 37 копеек?
Решение. Если число монет не превосходит семи, то сумма окажется не более 7·5 = 35 копеек. Поэтому семи и менее монет нам не хватит. Предположим, что монет восемь. Все они не могут быть пятикопеечными (8 · 5 = 40). Семь пятикопеечных монет и одна трёхкопеечная дают в сумме 38 копеек. Если же пятикопеечных монет не более шести, то сумма не превосходит 6·5+2·3 = 36 копеек. Значит, восемью монетами набрать 37 копеек также не получается. Итак, монет должно быть не менее девяти. Приведём пример подходящего набора из девяти монет: пять пятикопеечных и четыре трёхкопеечных (5 · 5 + 4 · 3 = 37). Следовательно, наименьшее возможное число монет равно девяти.
Натуральные числа от 1 до 10 разбили на две группы так, что произведение чисел в первой группе делится на произведение чисел во второй группе. Какое наименьшее значение может принимать частное от деления первого произведения на второе?
Каждое из чисел 2, 3, …, 7 умножили на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Наибольшее целое число, не превосходящее число х, равно 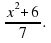 Найдите все такие значения x.
Найдите все такие значения x.
Длины сторон прямоугольника – натуральные числа, а его периметр равен 4000. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n ― также натуральное число.
а) Какое наибольшее значение может принимать площадь прямоугольника?
б) Какое наименьшее значение может принимать площадь прямоугольника?
в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n
Натуральные числа a, b, c и d удовлетворяют условию abcd.
а) Найдите a, b, c и d, если 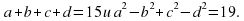
б) Может ли быть 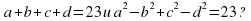
в) Пусть 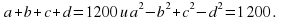 Найдите количество возможных значений числа а.
Найдите количество возможных значений числа а.
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, среднее арифметическое всех отрицательных из них равно −8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?


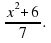
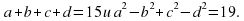
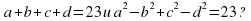
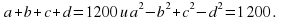 Найдите количество возможных значений числа а.
Найдите количество возможных значений числа а.