Параллелограмм и трапеция. Основные свойства и признаки.

Выпуклые четырехугольники

Выпуклый четырехугольник — четырехугольник, который расположен по одну сторону от любой из своих сторон.

Сумма углов выпуклого четырехугольника равна 360˚.

Средняя линия — отрезок прямой, соединяющий середины противоположных сторон.

Теоремы:

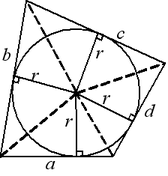
• Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы сумма длин противоположных сторон были равны друг другу. Центр окружности — точка пересечения биссектрис.

• Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны. Центр окружности — точка пересечения серединных перпендикуляров к сторонам четырехугольника.

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

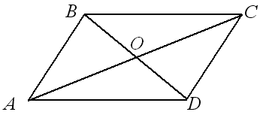
Теоремы (свойства параллелограмма):

• В параллелограмме противоположные стороны равны и противоположные углы равны: AB=CD, BC=AD, ,.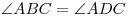

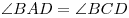• Диагонали параллелограмма точкой пересечения делятся пополам: AO=OC, OB=OD.

• Углы, прилежащие к любой стороне, в сумме равны 180˚.

• Диагонали параллелограмма делят его на два равных треугольника.

• Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC² + BD² = 2AB² + 2BC .

Признаки параллелограмма:

• Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

• Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Дополнительно:

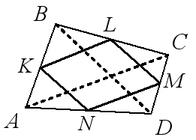
• Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,L,M,N являются вершинами параллелограмма Вариньона.

• Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника ABCD. Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства:

• Все свойства параллелограмма.

• Диагонали прямоугольника равны AC = BD.

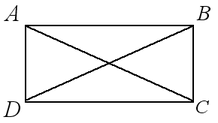
Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Помним: Вокруг прямоугольника всегда можно описать окружность.

Ромб — параллелограмм, у которого все стороны равны.

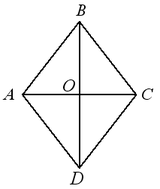
Свойства:

• Все свойства параллелограмма.

• Диагонали ромба взаимно перпендикулярны.

• Диагонали ромба делят углы ромба пополам.

Признаки ромба:

• Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.

• Если в параллелограмме диагонали делят углы пополам, то этот параллелограмм — ромб.

Помним: В ромб всегда можно вписать окружность.

Квадрат – параллелограмм, у которого все стороны равны и все углы — прямые; или прямоугольник, у которого все стороны равны; или ромб, у которого все углы — прямые.

Свойства:

• Все свойства прямоугольника и ромба.

• Диагонали квадрата равны

Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие -боковыми сторонами.

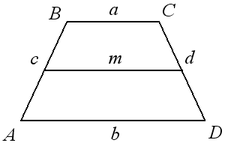
Высота трапеции — расстояние между прямыми, на которых лежат основания трапеции, любой общий перпендикуляр этих прямых.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон. 

Свойство трапеции:

Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон: a + b = c + d , а средняя линия равна полусумме боковых сторон: m = (c+d): 2 .

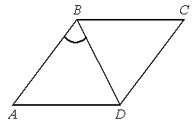
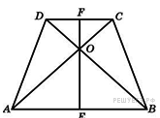
Равнобедренная трапеция — трапеция, у которой боковые стороны равны AB = CD. Тогда равны диагонали AC = BD и углы при основании  , .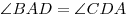

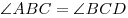Из всех трапеций только около равнобедренной трапеции можно описать окружность, так как окружность можно описать около четырехугольника, только если сумма противоположных углов равна 180˚.

В равнобедренной трапеции расстояние от вершины одного основания, до проекции противоположной вершины на прямую, содержащую это основание равно средней линии.

Прямоугольная трапеция — трапеция, у которой один из углов при основании равен 90˚.

Теоремы о площади четырехугольника

• Любой четырехугольник можно разбить на треугольники, и его площадь будет равна сумме площадей треугольников.

• Если в четырехугольник можно вписать окружность, то его площадь равна: S=pr.

• Если четырехугольник вписан в окружность,то его площадь будет равна

.

• Если диагонали выпуклого четырехугольника равны  и  и образуют угол,  то площадь четырехугольника равна: .

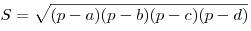Следствие: Площадь ромба равна: .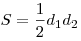

• Площадь квадрата: .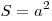

• Площадь прямоугольника: .

• Площадь параллелограмма: .

• Площадь трапеции: .