Программирование. Задачи на пересечение областей
На этом занятии рассмотрим связь между булевой логикой, теорией множеств и алгеброй функции
Задания по теме для самостоятельного решения
Задание 1
(2 балла)Какое из условий правильно определяет принадлежность точки на плоскости (х, у — действительные числа) заштрихованной области.
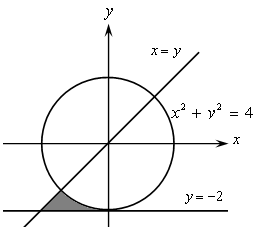
Варианты ответов:
1) (х * х + у * у >= 4) and (у >= −2) and (у <= х) and (х <= 0)
2) (х * х + у * у <= 4) and (у >= −2) and (у <= х) and (х <= 0)
3) (х * х + у * у >= 4) and (у >= −2) and (у <= х)
4) (х * х + у * у >= 4) and (у <= −2) and (у >= х) and (х <= 0)
Задание 2
(2 балла)Какое из условий правильно определяет принадлежность точки на плоскости (х, у — действительные числа) заштрихованной области.
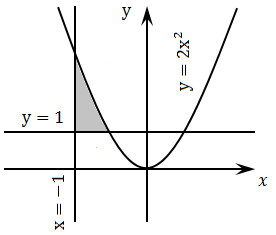
Варианты ответов:
1) (у <= 2 * х * х) and (х >= −1) and (у <= 1) and (х < 0)
2) (у <= 2 * х * х) and (х >= −1) and (у >= 1) and (х > 0)
3) (у <= 2 * х * х) or (х >= −1) or (у >= 1) and (х < 0)
4) (у <= 2 * х * х) and (х >= −1) and (у >= 1) and (х < 0)
Задание 3
(2 балла)Какое из условий правильно определяет принадлежность точки на плоскости (х, у — действительные числа) заштрихованной области.
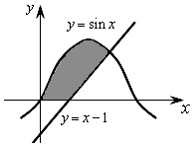
Варианты ответов:
1) (у <= sin(x)) and (у >= х − 1) and (у >= 0)
2) (у <= sin(x)) and (у >= х − 1) and (х >= 0)
3) (у >= sin(x)) and (у >= х − 1) and (у >= 0) and (х >= 0)
4) (у <= sin(x)) and (у >= х − 1) and (у >= 0) and (х >= 0)

