Инварианты. Полуинварианты.

ИНВАРИАНТЫ.

Такие задачи довольно часто встречаются на олимпиадах. Если не знать принцип их решения, то решить их довольно трудно. А надо всего лишь искать то, что не меняется при описанных преобразованиях.

Сначала рассмотрим классическую задачку на инвариант.

Задача. На столе стоят вверх дном семь стаканов. Разрешается переворачивать одновременно любые два стакана (разумеется, можно перевернуть любой стакан, стоящий вверх дном, так, чтобы он стоял на дне, а можно перевернуть любой стоящий правильно стакан так, чтобы он стал стоять вверх дном). Можно ли добиться того, чтобы все семь стаканов на столе стояли на дне?

Конечно же, сначала нужно попробовать переворачивать стаканы. Однако довольно быстро становится понятно, что так просто эта задачка не решается. Тогда возникает желание доказать, что добиться требуемой расстановки стаканов невозможно. Как это сделать? Давайте сравним количества стаканов, стоящих на дне и вверх дном. Сначала мы имеем 7 стаканов, которые стоят вверх дном и 0 стаканов, стоящих на дне. Мы можем перевернуть любые два стакана. Какие бы стаканы мы ни выбрали, у нас будет 5 стаканов вверх дном и 2 стакана, стоящих правильно. В следующий раз мы можем перевернуть стаканы различными способами. Так, мы можем поставить на дно два стакана, стоящих вверх дном. Тогда у нас останется 3 стакана, стоящих вверх дном, а 4 стакана будут стоять правильно. Мы можем перевернуть один стакан, стоящий вверх дном, и один стакан, стоящий правильно. Тогда ничего не изменится, и у нас останется 5 стаканов, стоящих вверх дном, и 2 стакана, стоящих на дне. И последний вариант: мы можем перевернуть два стакана, которые стоят на дне. Тогда получим исходную ситуацию, а именно 7 стаканов вверх дном и 0 стаканов, стоящих правильно.

Давайте посмотрим, что общего во всех этих ситуациях. Найдем разность числа стаканов, стоящих вверх дном, и числа стаканов, стоящих на дне. В исходном варианте эта разность равна семи. После первого переворачивания она становится равна трем. А дальше, в зависимости от выбранного варианта переворачивания стаканов, она станет равной -1, 3 или 7. Мы видим, что эта разность может измениться только на 4. И в данном случае неважно, что исходно мы рассматривали 7 стаканов, которые были перевернуты вверх дном. Если вы рассмотрите случай, когда a стаканов стоят на дне, а b стаканов — вверх дном, вы придете к тому же самому выводу. В качестве полезного и простого упражнения попробуйте сделать это сами. Предположим, что нам удалось, переворачивая стаканы, добиться их правильного расположения. Тогда в конечной ситуации разность между числом стаканов, стоящих вверх дном, и числом стаканов, стоящих правильно, равна -7. И мы видим, что число -7 отличается от 7 на 14 — это число не кратно 4. Следовательно, действуя описанным в условии задачи способом, добиться того, что все 7 стаканов будут стоять на дне, невозможно.

А теперь вернемся к непонятному слову инвариант. Оно имеет очень простое значение: то, что сохраняется, не изменяется при некоторых преобразованиях.

В рассмотренной задаче инвариантом был остаток от деления на 4 разности числа стаканов, стоящих вверх дном, и числа стаканов, стоящих на дне. Он должен всегда оставаться равным 3. При решении задач часто полезно знать следующие утверждения:

Лемма 1. Четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых.

Пример. Число 1 +2 + 3 + … + 10 – нечетное, так как в сумме 5 нечетных слагаемых.

Пример 2. Число 5 + 7 + 9 + 11 +13 + 15 – четное, так как в сумме 6 нечетных слагаемых.

Лемма 2. Знак произведения нескольких (отличных от 0) чисел определяется четностью количества отрицательных сомножителей.

Задачи к уроку.

Задача 1. Не вычисляя сумму a) 1 + 2 + 3 + ... + 2017; 
b) 12+22+32+...+2015212+22+32+...+20152, скажите, является она четной или нет.

Задача 2. Существуют ли целые числа a и b, такие что ab(a+b)=201500010002017?

Задача 3. Автомат при опускании гривенника выбрасывает пять двушек, а при опускании двушки – пять гривенников. Может ли Петя, подойдя к автомату с одной двушкой, получить после нескольких опусканий одинаковое количество двушек и гривенников?

Задача 4. Даны три числа: 2015, 2016 и 2017. За один ход разрешается заменить числа 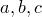 на числа 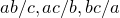. Можно ли через несколько ходов получить числа 2018, 2019 и 2020?

Задача 5. Вдоль забора растут восемь кустов малины. Число ягод на соседних кустах отличается на единицу.  Может ли на всех кустах быть вместе 2015 ягод?

Задача 6. Парламент состоит из двух равных по численности палат. На совместном заседании голосовали все, и никто не воздержался при голосовании. Когда спикер объявил, что решение принято большинством в 23 голоса, оппозиция закричала:  Почему?

Задача 7. На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными?

Задача 8. 100 фишек выставлены в ряд. Разрешено менять местами две фишки, стоящие через одну фишку. Можно ли с помощью таких операций переставить все фишки в обратном порядке?

Задача 9. Лягушка прыгает вдоль прямой̆. Сначала она прыгнула на 1 см, затем на 3 см в том же или в противоположном направлении, затем на 5 см в том же или в другом направлении и т. д. Могло ли случиться так, что она оказалась в исходной̆ точке после 57-го своего прыжка?

Задача 10. Миша написал на доске в некотором порядке 2016 плюса и 2017 минусов. Время от времени Юра подходит к доске, стирает любые два знака и пишет вместо них один, причем если он стер одинаковые знаки, то вместо них он пишет плюс, а если разные, то минус. После нескольких таких действий̆ на доске остался только один знак. Какой̆?

Задача 11. Дана квадратная таблица 4*4, в каждой клетке которой стоит знак "+" или "-":
 

За один ход можно поменять знаки на противоположные в любой строке или любом столбце. Можно ли через несколько ходов получить таблицу из одних плюсов?

Задача 12. Вася разозлился на карикатуру в школьной газете и порвал ее на 4 части, затем взял один из получившихся кусочков и тоже порвал на 4 части, затем снова взял один из кусочков – и так до тех пор, пока вся злость не вышла. Могло ли у Васи вконце получиться 2016 клочков бумаги? А 2017?

Задача 13. 2000 чисел х₁, х₂,…, х₂₀₀₀ записаны в строчку. Известно, что сумма любых трех соседних из них равна 200. При этом первое число равно 19, последнее 98. Найдите остальные 1998 чисел.

Задача 14. В трех кучках лежат 1,9 и 98 камней. За один ход разрешается из любых двух кучек взять по одному камню и переложить в третью, можно ли за несколько ходов собрать все камни в одной из кучек?

Задача 15. На острове Серобуромалин живет 13 серых, 15 бурых и 17 малиновых хамелеонов. Когда встречаются два хамелеона разного цвета, они одновременно перекрашиваются в третий цвет. Может ли через некоторое время оказаться, что все хамелеоны имеют один цвет?

Задача 16. Круг разделен на шесть секторов. В каждом секторе написано число. Разрешается одновременно увеличивать числа в двух соседних секторах на один. Можно ли сделать все числа равными, если в начале они такие: 1,0,1,0,0,0?

Задача 17. Каждое число от 1 до 1000000 заменили суммой его цифр. С полученным набором чисел проделали то же самое, и так до тех пор, пока не получилось 1000000 однозначных чисел. Каких чисел получилось больше: единиц или двоек?