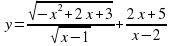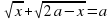Математика 10, 11 классы

Подготовка к ЕГЭ, (бывшая С) (2017)

ЕГЭ по математике в нашей стране является обязательным, и если одним учащимся он нужен лишь для получения аттестата, то другие тратят неимоверные силы и средства для достижения цели – максимального балла на профильном ЕГЭ, ведь это существенно увеличивает шансы поступить на бюджет в лучшие ВУЗы России.

Мы приглашаем вас на курс подготовки к сложной части ЕГЭ по математике (части С). Курс рассчитан на тех, кто достаточно владеет теорией, но имеет малую практику в решении задач, тех, кто хочет интенсивно повторить основные темы математики и набрать максимально возможные баллы на ЕГЭ. Последние семь задач ЕГЭ приносят большие баллы, но и требуют большой отдачи и максимальной концентрации, ведь каждая, пусть даже малая, ошибка ведет к снижению баллов.

На курсе мы научимся не терять баллы за глупые ошибки и оформление, вместе отработаем решение как типичных, так и сложных задач, научимся ценить время, ведь на экзамене оно ограничено. Все это позволит вам подойти к экзамену собранными, сконцентрированными и уверенными в своих силах.

от 30

рублей
за занятие

Разбор задач 13-19 ЕГЭ 2016 (профиль)

На этом занятии мы рассмотрим задания 13-19 ЕГЭ 2016 и поговорим о методах их решения.

Нажмите на картинку, чтобы посмотреть видео этого занятия

Конспект занятия "Разбор задач 13-19 ЕГЭ 2016 (профиль)"

Задания ЕГЭ по математике 2016 (профиль).

13. а) Решите уравнение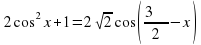

б) Укажите корни этого уравнения, принадлежащие промежутку .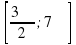

14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ AB=AA₁=6, BC=4. Точка Р - середина ребра АВ, точка М лежит на ребре DD₁ так, что DM:D₁D=2:3.

а) Докажите, что прямая BD₁ параллельна плоскости MPC.

б) Найдите площадь сечения параллелепипеда плоскостью MPC.

15. Решите неравенство:

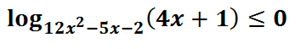
Подсказка: используем определение логарифма для нахождения ОДЗ и метод рационализации для перехода от логарифмического неравенства к обычному.

16. В остроугольном треугольнике ABC проведены выстоты AK и BP.

а) Докажите, что углы АКР и АВР равны.

б) Найдите длину отрезка РК, если известно, что АВ=5, ВС=6, СА=4.

17. В распоряжени прораба Валерия имеется бригада каменщиков в составе 40 человек. Их нужно распределить на неделю на два строящихся объекта.

Если на первом объекте работает t человек, то их недельная зарплата составляет 1,5t² тыс. рублей.

Если на втором объекте работает t человек, то их недельная зарплата составляет 2t² тыс. рублей.

Как Валерию нужно распределить на эти объекты бригаду каменщиков, чтобы выплаты на их недельную зарплату оказались наименьшими? Сколько рублей в этом случае пойдет на зарплату?

18. Найдите все значения параметра а, при которых уравнение имеет один корень:

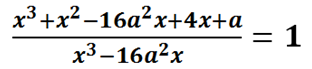
19. На доске написаны числа 1, 2, 3, …, 30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стертых на предыдущих ходах.

а) Приведите пример последовательности 5 ходов.

б) Можно ли сделать 10 ходов?

в) Какое наибольшее число ходов можно сделать?

Домашнее задание:

№1. а) Решите уравнение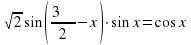

б) Найдите все корни этого уравнения, принадлежащие промежутку .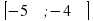

В ответ укажите количество корней, найденных в пункте б.

№2. В правильной треугольной призме ABCA₁B₁C₁ сторона основания AB равна 6, а боковое ребро АА₁ равно 3. На ребре АВ отмечена точка К так, что АК=1. Точки М и L – середины ребер А₁С₁ и В₁С₁ соответственно. Плоскость β параллельна прямой АС и содержит точки К и L.

а) Докажите, что прямая ВМ перпендикулярна плоскости β.

б) Найдите расстояние от точки С до плоскости β.

В ответ укажите найденное расстояние, увеличенное в 4 раза, числом без знаков препинания.

№3. Укажите область определения функции:

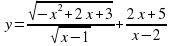
В ответ запишите сумму целых чисел из найденного интервала.

№4. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер? В ответ укажите доход числом в миллионах рублей без знаков препинания.

№5. Найдите все значения a, при каждом из которых уравнение

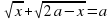
имеет ровно два различных корня.

В ответ укажите сумму целых значений параметра.

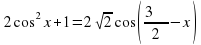
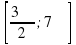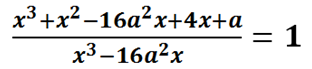
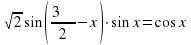
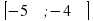Задания по теме для самостоятельного решения

Задание 1

(1 балл)

а) Решите уравнение $\sqrt{2} \sin (\frac{3 π}{2} - x) \cdot \sin x = \cos x$

б) Найдите все корни этого уравнения, принадлежащие промежутку $[- 5 π; - 4 π]$ .

В ответ укажите количество корней, найденных в пункте б.

Задание 2

(2 балла)

В правильной треугольной призме ABCA₁B₁C₁ сторона основания AB равна 6, а боковое ребро АА₁ равно 3. На ребре АВ отмечена точка К так, что АК=1. Точки М и L – середины ребер А₁С₁ и В₁С₁ соответственно. Плоскость β параллельна прямой АС и содержит точки К и L.

а) Докажите, что прямая ВМ перпендикулярна плоскости β.

б) Найдите расстояние от точки С до плоскости β.

В ответ укажите найденное расстояние, увеличенное в 4 раза, числом без знаков препинания.

Задание 3

(2 балла)

Укажите область определения функции:

$y = \frac{\sqrt{- x^{2} + 2 x + 3}}{\sqrt{x - 1}} + \frac{2 x + 5}{x - 2}$

В ответ запишите сумму целых чисел из найденного интервала.

Проверить правильность выполнения заданий вы можете в автоматическом режиме в разделе домашние задания на странице с курсом "Математика Подготовка к ЕГЭ, (бывшая С) 2017"

Следующий урок на тему " Задача 17. Текстовые задачи. Проценты."