Основные понятия теории вероятностей
1. Случайное событие - это любое событие, которое может либо произойти, либо не произойти.
Например,
2. Равновозможные события - это такие события, когда есть основания считать, что ни одно из них не более вероятно, чем другие.
Например,
3. Испытание - это какое-то действие, которое происходит в условии данной задачи.
Примеры испытаний:
В этих примерах:
выстрел - это испытание, а попал или промахнулся - это событие;
4. Элементарный исход - это каждый результат какого-либо испытания. Например,
5. Несовместные события - такие события, когда появление одного испытания исключает появление другого испытания.
Например,
попадание - промах;
"орёл - решка",
выпало 5 очков - выпало 2 очка;
наступила весна - наступило лето, (т.е. события не могут случиться одновременно).
6. Совместные события - такие события, которые могут произойти одновременно.
Например,
наступило утро, и пошёл снег;
один стрелок попал в цель, а другой стрелок не попал в цель;
7. Независимые события - это те события, которые происходят независимо друг от друга.
Например,
при бросании двух игральных костей: на первой кости выпало 5 очков независимо от того, сколько очков выпало на второй кости;
при бросании двух монет на одной монете выпал "орёл", а на другой может выпасть как "орёл", так и "решка";
от того, что первый стрелок попал в цель не зависит попал или промахнулся второй стрелок.
В отличии от ситуации, когда от исхода первого события зависит исход второго события.
Вот, например,
8. Группа событий называется полной, если в результате испытаний, появится хотя бы одно из событий.
Например,
"попадание - промах" составляют полную группу событий;
"орёл - решка" составляют полную группу событий;
1,2,3,4,5,6 очков на игральной кости составляют полную группу событий.
9. Вероятностью события А называется отношение благоприятствующих исходов к числу равновозможных событий:
Р (А) = 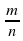
10. Суммой двух несовместных событий А и В называется появление хотя бы одного из этих событий (или события А, или события В).
11. Теорема о сумме двух несовместных событий
Если А и В - несовместные события, т.е. события, которые не могут случиться одновременно, то
P (A+B) = P (A) + P (B).
12. Следствие 1 из теоремы о сумме двух несовместных событий.
Если A, B, С, D, ..., Z - несовместные события, то
P (A+B+C+...+Z) = P (A) + P (B ) + P (C) + ...+ P (Z).
13. Следствие 2 (о полной группе событий)
Если события A, B, C, D, E, F образуют полную группу событий:
(например, выпало 1, 2, 3, 4, 5, 6 очков при бросании игральной кости),
то сумма вероятностей событий А, В, С, D, E, F равна единице.
P (A) + P (B) + P (C) + P (D) + P (E) + P (F) = 1.
14. Следствие 3 (о противоположных событиях)
P (A) + P (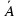 ) = 1.
) = 1.
Где используется эта формула?
15. Произведение независимых событий А и В - это событие, когда произошло и событие А, и событие В.
Например,
16. Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий
P (A ∙ B) = P (A) ∙ P (B).
Эта формула верна исключительно для независимых событий.
16. Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий А и В минус вероятность произведения событий А и В.
P (A+B) = P (A) + P (B) - P (A ∙ B).
событие А+B - произошло либо событие А, либо событие В; А - произошло только событие А;
В - произошло только событие В; А ∙ В - произошло и событие А, и событие В (это возможно, так как события А и В могут произойти независимо друг от друга).


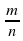
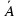 - полная группа событий (попадание-промах, "орёл"-"решка"), то
- полная группа событий (попадание-промах, "орёл"-"решка"), то