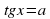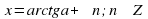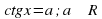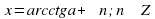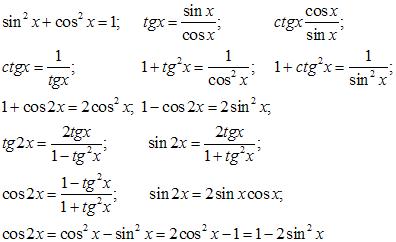Решение тригонометрических уравнений. Выбор корней.
Тригонометрические уравнения – наиболее распространенные уравнения в задаче 13.
Любое тригонометрическое уравнение в процессе решения с помощью надлежащих преобразований должно быть приведено к простейшим.
Решение простейших тригонометрических уравнений
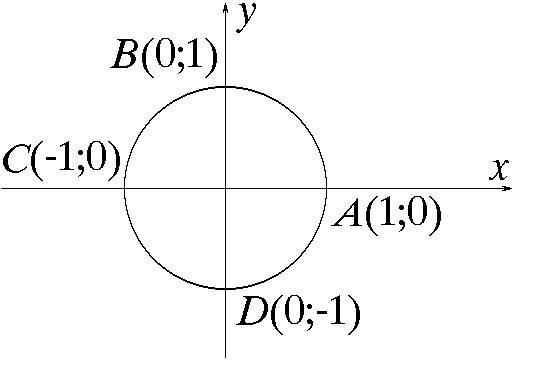
Частные случаи:
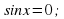
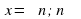 Z
Z
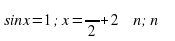 Z
Z
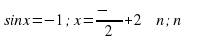 Z
Z
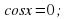
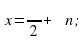
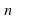 Z
Z
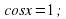
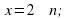
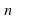 Z
Z
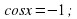
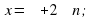
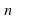 Z
Z
Решение уравнения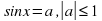
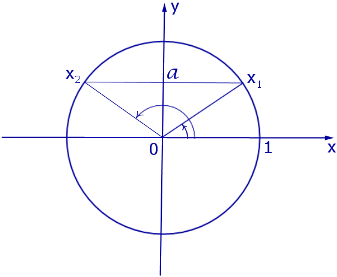
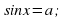
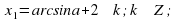
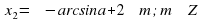
Обычная форма записи решения
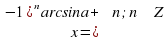
Помним, если 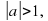 то уравнение
то уравнение 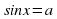 не имеет корней.
не имеет корней.
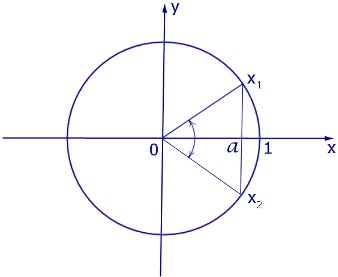
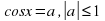
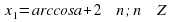
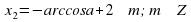
Обычная форма записи решения
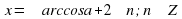
Помним, если 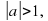 то уравнение
то уравнение 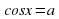 не имеет корней.
не имеет корней.
Решение уравнения 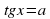
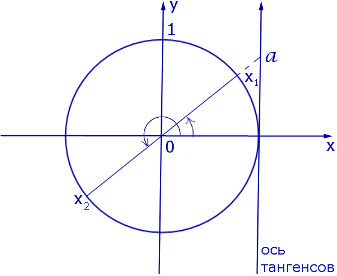
Обычная форма записи решения
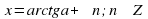
Решение уравнения 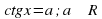
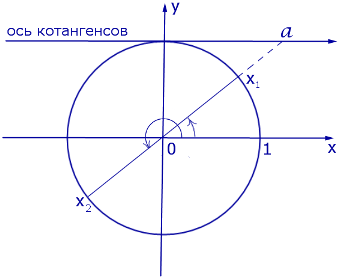
Обычная форма записи решения
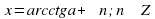
Наиболее часто при решении тригонометрических уравнений применяются следующие методы:
разложение на множители;
способ замены (сведение к алгебраическим уравнениям);
сведение к уравнениям, однородным относительно 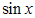 и
и 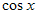 ;
;
преобразование суммы тригонометрических функций в произведение;
преобразование произведения тригонометрических функций в сумму;
использование формул понижения степени;
равенство одноименных тригонометрических функций;
равенство одноименных тригонометрических функций
введение вспомогательного аргумента.
При этом, как правило, в процессе решения тригонометрического уравнения приходится использовать не один, а несколько из указанных выше методов.
Способ замены
Данным методом решаются уравнения вида 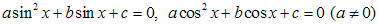 ,
, 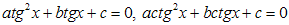 .
.
Они сводятся к простейшим тригонометрическим уравнениям с помощью замены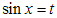 или
или 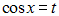 . Уравнения
. Уравнения 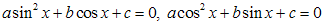 не являются с виду алгебраическими, но их можно свести к алгебраическим:
не являются с виду алгебраическими, но их можно свести к алгебраическим: 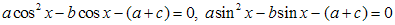 .
.
При решении уравнений этим методом необходимо знать формулы:
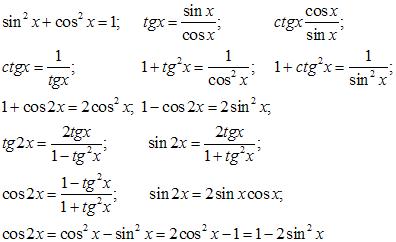
Однородные уравнения
Уравнения:
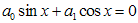 ,
,
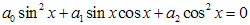 ,
,
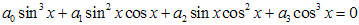 ,
,
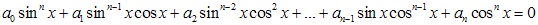
называются однородными относительно 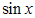 и
и 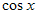 . Они обладают тем свойством, что сумма показаний степеней при
. Они обладают тем свойством, что сумма показаний степеней при 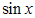 и
и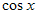 у всех членов уравнения одинакова. Делением на
у всех членов уравнения одинакова. Делением на  соответственно уравнения приводятся к алгебраическим уравнениям относительно
соответственно уравнения приводятся к алгебраическим уравнениям относительно  . При этом, конечно, предполагается, что коэффициент
. При этом, конечно, предполагается, что коэффициент  . В результате получаем равносильное уравнение, так как разделили на
. В результате получаем равносильное уравнение, так как разделили на  (если бы
(если бы  , то из исходного уравнения следует, что и
, то из исходного уравнения следует, что и , а это невозможно, так как
, а это невозможно, так как 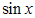 и
и 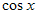 при одном и том же значении х в нуль не обращаются, ибо всегда
при одном и том же значении х в нуль не обращаются, ибо всегда ).
).
Уравнение легко сводится к однородному, если правую часть представить в виде . После очевидных преобразований получаем
. После очевидных преобразований получаем
.
Разложение на множители
При решении уравнений этим методом нужно пользоваться известными способами разложения на множители алгебраических выражений. Необходимо также знать уже приведенные формулы и дополнительно:
Преобразование суммы тригонометрических функций в произведение
При решение уравнений данным способом необходимо знать формулы:
Преобразование произведения тригонометрических функций в сумму
При решение уравнений данным способом необходимо знать формулы:
Использование формул понижения степени
При решение уравнений данным способом необходимо знать формулы:
Введение вспомогательного аргумента
Метод основан на преобразовании выражения  , где a и b – постоянные, не обращающиеся в нуль одновременно.
, где a и b – постоянные, не обращающиеся в нуль одновременно.
Введем угол  , положив
, положив
.
Тогда:
,
где  находится из уравнения
находится из уравнения  .
.
Метод рационализации для уравнения вида 
Метод универсальной тригонометрической подстановки
Известно, что если  , то
, то  выражаются рационально через
выражаются рационально через  .
.
Вводим вспомогательное неизвестное так, чтобы после подстановки получилось рациональное уравнение относительно вспомогательного неизвестного.
Данное уравнение можно переписать в виде
.
Положим  , тогда получим
, тогда получим
 .
.
Решим данное уравнение и получим следующие ответы
1. если  , то у уравнения нет корней;
, то у уравнения нет корней;
2. если  , то ;
, то ;
3. если  , то .
, то .
Приведение к однородному для уравнения вида 
Данное уравнение перепишем в виде
,
т.е. имеем однородное уравнение
.
Задачи к теме:
Разложение на множители:
Решить уравнение  .
.
Решить уравнение  .
.
Метод разложения на множители с использованием формул преобразования суммы в произведение и произведения в сумму.
Решите уравнение: 
Решить уравнение  Найти все корни, принадлежащие промежутку
Найти все корни, принадлежащие промежутку  .
.
Решить уравнение  .
.
Замена переменной:
Решить уравнение  .
.
Решить уравнение  .
.
Однородные уравнения и сводимые к ним:
Решить уравнение: .
.
а) Решите уравнение .
б) Найдите количество корней этого уравнения, принадлежащих промежутку .
Преобразование суммы в произведение и произведения в сумму:
Решить уравнение .
Решить уравнение  .
.
Решить уравнение  .
.
Формулы понижения степени:
Решить уравнение:
.
Введение вспомогательного угла:
Решить уравнение  .
.
Решить уравнение  .
.
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку .
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку.
. В ответе напишите наименьший положительный корень, умноженный на 2.



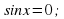
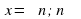
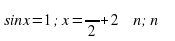
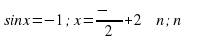
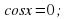
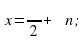
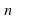
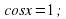
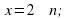
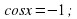
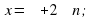
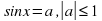

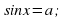
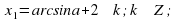
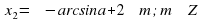
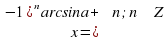
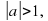 то уравнение
то уравнение 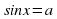 не имеет корней.
не имеет корней. 
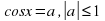
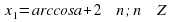
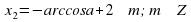
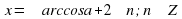
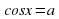 не имеет корней.
не имеет корней.